Принцип наименьшего действия

При исследования движения материальных частиц мы будем находить из принципа наименьшего действия. Этот принцип заключается, как известно, в том, что для всякой механической системы существует такой интервал S, называемый действием, который для истинного движения имеет минимум и вариация которого, следовательно, равна нулю.

Определим интеграл действия для свободной материальной частицы, т.е частицы не находящиеся под действием каких-либо внешних сил. Заметим, что этот интеграл не должен зависеть от выбора той или иной и.с.о., т.е. он должен быть инвариантом относительно преобразования Лоренца. Отсюда следует, что он должен быть взят от скаляра. Далее, ясно, что под интегралом должны стоять дифференциалы в первой степени. Однако единственный такой скаляр, который можно построить для свободной материальной частицы, есть интервал ds или , где - некоторая постоянная. Итак, действие для свободной частицы должно иметь вид

Где обозначает интервал вдоль мировой линии между двумя заданными событиями- нахождением частицы в начальном и конечном местах в определенные моменты и 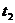времени, т.е. между заданными мировыми точками; есть некоторая постоянная, характеризующая частицу. Легко видеть, что . В самом деле, в § 2 мы видим, что имеет мах значение вдоль прямой мировой линии; интегрируя вдоль кривой мировой линии, можно сделать его сколь угодно малым. Таким образом, , взятый с положительным знаком, не может иметь минимума, взятый же с обратным знаком, он, очевидно, имеет минимум – вдоль прямой мировой линии.

Действие можно представить также в виде

Где L – называется, как известно, функции Лагранжа данной механической системы. С помощью (1.12) мы находим

Где 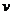- скорость материальной частицы. Функция Лагранжа для частицы есть, т.о,

При предельном переходе 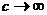наше выражение для должно, очевидно перейти в классическое выражение: . Для осуществления этого перехода разложим в ряд по степеням .

Как известно, в функции Лагранжа несущественны члены, являющийся полными производными от произвольных функций. Всякая постоянная является полной производной от этой же постоянной, уменьшенной на время, поэтому в ее можно опустить. Отсюда

, т.е.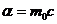

Итак, действие для свободной материальной точки равно

(2.1)

а функция Лагранжа

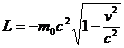(2.2)

Не нашли, что искали? Воспользуйтесь поиском: