Преобразование скорости.

Пусть система движется относительно системы со скоростью V вдоль оси X. Пусть 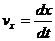есть компонента скорости частицы в системе , а 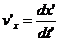компонента скорости той же частицы в системе . Из (1.13) имеем:

Разделив первые три равенства на четвертое, находим

или

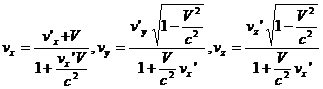(1.18)

Эти формулы и определяют преобразование скорости. При 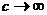имеем классические формулы сложения скоростей .

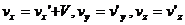Если частица движется параллельно оси x, то , 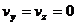. Тогда 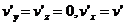, причем

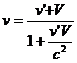(1.19)

Легко убедиться в том, что сумма двух скоростей, меньших или равных скорости света, есть согласно этой формуле снова скорость, не большая скорости света. Для скоростей V значительно меньших скорости света (скорость может быть любой) имеем приближенно с точностью до членов порядка V/c

, ,

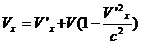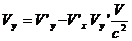Эти три формулы можно записать в виде одной векторной формулы

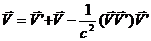(1.20)

Выберем оси координат так, чтобы скорость частицы в данный момент лежала в плоскости .Тогда скорость частицы в системе K имеет компоненты 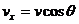, , 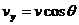, 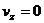а в системе 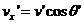, , 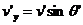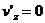( 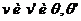- модули скорости и углы, образованные, с осями X и X’ соответственно в системе и ). С помощью формулы (1.20) находим

(1.21)

Эта формула определяет изменение направления скорости при переходе от одной системы отсчета к другой.

Рассмотрим подробнее важный частный случай этой формулы, а именно отклонение света при переходе к другой системе отсчета, явление, называемое аберрацией света. В этом случае и (1.21) переходит в

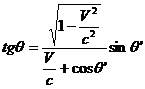(1.22)

Из тех же формул (1.18) легко получить аналогичную зависимость для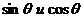

(1.23)

В случае находим из этих формул с точностью до членов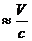

Вводя угол 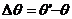(угол аберрации), находим с той же точностью

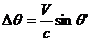(1.24)

т.е. известную элементарную формулу для аберрации света.

Не нашли, что искали? Воспользуйтесь поиском: