Электростатическая энергия зарядов.

Определим энергию системы зарядов. При этом будем исходить из представления об энергии поля, то есть из выражения (3.88) для плотности энергии. Именно энергия системы зарядов должна быть равна

где есть поле, создаваемое этими зарядами, интеграл берется по всему пространству. Подставим сюда 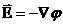, можно записать

В связи с тем, что имеем

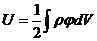
(4.12)

Для системы точечных зарядов можно вместо интеграла написать сумму по зарядам

(4.13)

где 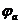- потенциал поля, создаваемого всеми зарядами в точке, где находится заряд .

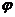В случае одного точечного заряда получаем, что частица должна обладать «собственной» потенциальной энергией, равной , где - потенциал, создаваемый зарядом в точке, в которой он сам находится. Но и при . Таким образом, точечный электрический заряд в электродинамике обладает бесконечной «собственной» энергией, а следовательно и бесконечной массой. Следует заметить, что в соответствии с теорией относительности всякую элементарную частицу надо рассматривать как точечную.

В самом деле. В рамках неквантовой механики элементарной частицей называется частица, механическое состояние которой определяется заданием трех координат и трех компонент скорости движения частицы как целого. Поэтому, если бы частица была протяженной, то она должна быть одновременно абсолютно твердой (недеформируемой). В противном случае указанное описание механического состояния было бы невозможным (при деформации имеет место независимое движение отдельных частей протяженного тела). Однако в соответствии с теорией относительности абсолютно твердых тел быть не может. В самом деле. Пусть какое-то твердое тело внешним воздействием со стороны в какой-нибудь точке приводится в движение. Если бы тело было абсолютно твердым, то все его точки должны были бы прийти в движение одновременно с той, которая подверглась воздействию; в противном случае тело деформировалось бы. Теория относительности, однако, делает это невозможным, т.к. воздействие от данной точки передается к остальным с конечной скоростью, а потому все точки не могут начать одновременно двигаться. Таким образом, абсолютно твердых тел быть не может.

Таким образом, мы приходим к выводу, что электрон, например, обладает бесконечной массой. Физическая бессмысленность этого результата показывает, что уже основные принципы релятивистской электродинамики приводят к тому, что ее применимость должна быть ограниченной. Поскольку возникновение не имеющего физического смысла бесконечной «собственной энергии» элементарной частицы связано с тем, что такую частицу надо рассматривать как точечную, мы можем заключить, что электродинамика как логически замкнутая физическая теория становится внутренне – противоречивой при переходе к достаточно малым расстояниям. Можно оценить порядок этих расстояний. Правильная собственная энергия электрона должна быть порядка ; с другой стороны, при протяженном электроне «радиуса» собственная энергия электрона должна быть порядка 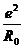. Таким образом, 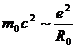, а отсюда

(4.14)

Эти размеры определяют границы применимости электродинамики к электрону, следующие уже из ее собственных принципов. Надо, однако, иметь в виду, что в следствие наличия квантовых явлений пределы применимости нашей электродинамики лежат гораздо выше. Квантовые эффекты становятся заметными на расстояниях ~ , где h – постоянная Планка.

Вернемся однако к системе зарядов и формуле (4.13). Стоящие в ней потенциалы 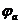согласно Кулону равны

(4.15)

- расстояние между зарядами . Выражение (4.13) состоит, т.о., из двух частей. Во-первых, оно содержит бесконечную постоянную - «собственную» энергию зарядов, - не зависящую от их взаимного расстояния. Вторая часть есть энергия взаимодействия зарядов, зависящая от их расположения. Только эта часть и представляет, очевидно, физический интерес. Она равна

(4.16)

или что тоже

(4.17)     (4.18)

В частности для двух зарядов имеем энергию

(4.19)

Дипольный момент.

Рассмотрим поле, создаваемое системой зарядов на больших расстояниях, т.е. на расстояниях, больших по сравнению с размерами системы.

Введем систему координат с началом где-нибудь внутри системы зарядов. Радиусы – векторы отдельных зарядов пусть будет . Потенциал поля, создаваемого всеми зарядами в точке с радиусом – вектором 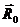, равен

(4.20)

суммирование производится по всем зарядам.

Мы должны исследовать это выражение при больших . Для этого разложим его в ряд по степеням , воспользовавшись формулой

(в дифференцирование производится по координатам конца вектора 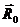) с точностью до членов первого порядка имеем

(4.21)

сумма

(4.22)

носит название дипольного момента системы зарядов. Существенно отметить, что если сумма всех зарядов равна нулю, то дипольный момент не зависит от выбора начала координат. Действительно, радиус – векторы и одного и того же заряда в двух разных системах связаны друг с другом соотношением

где некоторый постоянный вектор. Поэтому

Если обозначить посредством положительные и отрицательные заряды системы и их радиус – векторы, то можно написать дипольный момент в виде

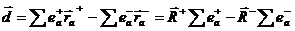
(4.23)

где

(4.24)

радиус-векторы «центров зарядов» положительных и отрицательных. Если , то

(4.25)

есть радиус-вектор от центра отрицательных к центру положительных зарядов. В частности, если имеются всего два заряда, то есть радиус-вектор между ними.

Если полный заряд равен нулю, то потенциал поля на больших расстояниях, как это следует из (4.21).

(4.26)

Напряженность поля имеет вид

или окончательно

(4.27)

где 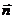- единичный вектор в направлении .

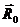Эквивалентная формула

(4.27’)

Полезна и следующая формула для напряженности

(4.28)

имеющая место до выполнения дифференцирования.

Итак, потенциал поля, создаваемого системой с равным нулю полным зарядом, на больших расстояниях обратно пропорциональна квадрату, а напряженность – кубу расстояния. Это поле обладает аксиальной симметрией вокруг направления 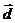. В плоскости, проходящей через это направление (которое выберем в качестве оси Z), компоненты вектора имеют вид

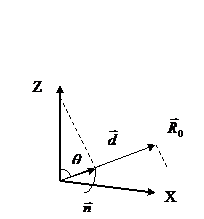
Из (4.27) следует

Проекция на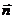

проекция на вектор .

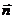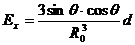
(4.29)

Радиальная и тангенциальная составляющие в этой плоскости

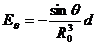
(4.30)

Не нашли, что искали? Воспользуйтесь поиском: