Глава 1. Макроскопическое описание и макроскопические характеристики поля

Электродинамика при наличии вещества в поле и необходимость макроскопического описания. Усреднение микроскопических характеристик. Символическая система уравнений Максвелла для поля в среде.

Предмет макроскопической электродинамики составляет изучение электромагнитных полей в пространстве, заполненном частично или полностью веществом- материальной средой.

При рассмотрении поля в среде, вообще говоря, надо было бы записать уравнения Максвелла для электромагнитных полей, создаваемых всеми зарядами в пространстве, в том числе, в веществе. К ним нужно добавить квантовомеханические уравнения движения всех зарядов. Затем все эти уравнения надо решать совместно. Такой подход называется микроскопическим, так как он учитывает процессы атомного масштаба.

Совершенно ясно, что такой подход невозможен (в одном моле вещества находится ~ зарядов) и на самом деле не нужен.

Дело в том, что измеряемое на опыте электромагнитное поле в веществе существенно меняется на расстояниях, значительно превышающих межатомные расстояния. Поэтому для величин, наблюдаемых на опыте, разница в положениях атомов мало существенна и среду из атомов можно рассматривать как сплошную среду. В этом и заключается так называемый феноменологический, макроскопический подход.

Рассмотрим переход от микроскопического описания электромагнитного поля в веществе к макроскопическому более детально. Выпишем микроскопические (истинные) уравнения Максвелла, полученные в части 1курса

(1)

и уравнение непрерывности (является следствием 2-го и 3-го уравнений)

Все величины, входящие в эти уравнения есть функции от , где - радиус-векторов геометрических точек пространства, t- мгновенные моменты времени. Здесь - микроскопические напряженности электрического и магнитного полей, - микроскопические значения плотностей заряда и тока. Они связаны с зарядами соотношениями:

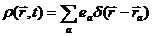
	(2),

где - радиус – вектор заряда , - его скорость.

В веществе все величины, в том числе и микроскопическое поле, весьма быстро меняются от точки к точке и в данном месте – во времени. Например, электрическое поле имеет сравнительно малое значение вне данного атома, но очень велико внутри атома и вновь спадает за его пределами. Рост поля в миллионы раз и его последующее спадание происходит в масштабах порядка атомных размеров. Такое же изменение поля во времени в фиксированной точке происходит, например, из-за теплового движения атома за очень малые доли секунды.

Поэтому интерес и значения имеют лишь средние значения соответствующих величин. Таким образом, надо произвести усреднение системы микроскопических уравнений (1), плотностей (2) и в связи с этим вводится понятие физически бесконечно малого объема и физически бесконечно малого интервала времени , по которым и будет проводиться это усреднение.

«Физически бесконечно малый объем » - это объем, диаметр которого велик по сравнению с межатомным расстоянием, однако мал по сравнению с расстояниями, на которых получающиеся в результате усреднения макроскопические величины меняются заметно.

«Физически бесконечно малый интервал времени » - это интервал много больший тех миллионных долей секунды, за которые происходит изменение микроскопических значений поля во времени в фиксированной точке пространства, например, из-за теплового движения атомов. Вместе с тем очень мал по сравнению со временем, за которое в фиксированной точке возникающие в результате макроскопические характеристики меняются заметно.

Процедура усреднения величины может быть представлена формулой:

(3)

Процедура (3) обладает следующими свойствами:

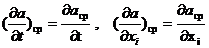
(4)

Проведем теперь усреднение системы (1), при этом обозначим

	(5)

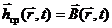
называют электрической напряженностью поля в среде, - магнитной индукцией поля в среде. Тогда вместо (1) имеем с учетом (3-5)

	(6)

Проведенное усреднение имеет пока что символический характер, т.к. находятся из этих уравнений, если известны . Однако средние значения плотностей тока и заряда неизвестны. Дело в том, что при усреднении, т.е. «размазывании» отрицательных и положительных зарядов, например, по физически бесконечно малому объему в большинстве случаев они компенсируют друг друга. Поэтому, например, средняя плотность заряда в отличие от микроскопической плотности равна нулю. Однако под действием макроскопических полей характер движения и расположения зарядов меняется, и средняя плотность становится отличной от нуля. Таким образом, средние плотности зарядов и токов зависят от существующих в веществе полей и 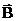и типа самого вещества и не могут быть заданы произвольно. Поэтому следующей проблемой является раскрытие этих зависимостей. В этом и заключается задача построения неформальной системы макроскопических уравнений.

Не нашли, что искали? Воспользуйтесь поиском: