Энергетические характеристики диэлектрика в электростатическом поле (термодинамические соотношения).

Вопрос об изменении термодинамических свойств, благодаря наличию электростатическое поля не возникает для проводников. Дело в том, что электростатичес кое поле внутри проводника есть нуль, и все изменения его термодинамических величин сводится просто к добавлению энергии, создаваемого им в окружающем пространстве поля к его полной энергии. Эта величина вообще не зависит от термодинамического состояния (в частности, от температуры) тела и потому, например, не сказывается на его энтропии. Напротив, в диэлектрике поле отлично от нуля внутри диэлектрика и его значение существенно зависит от термодинамического состояния диэлектрика. В тоже время это поле само оказывает влияние на термодинамические характеристики диэлектрика. Именно поэтому диэлектрик обладает несколькими энергетическими характеристиками. Так, если диэлектрик теплоизолирован, то удобно пользоваться внутренней энергией U, если процесс изменения поля происходит при T=const, то пользуются свободной энергией F и т.д.

Будем далее исходить из основного уравнения термодинамики для равновесного процесса

(3.11)

где δА - (бесконечно малая) работа, совершаемая над телом внешними силами.

Пусть в качестве этих сил служат электрические силы и пусть тело не деформируется (это ограничение на процесс). Конкретизируем источник этих сил. Пусть они создаются заряженными проводниками вне диэлектрика. Для конечного результата неважно, что является источником сил, каким образом они создаются.

Изменение электростатического поля в диэлектрике можно произвести, если изменить заряд проводника q на величину δq (δq вносится на поверхность проводника из бесконечности). Тогда работа по изменению заряда есть:

Но это и есть работа по изменению поля, т.е. в конце концов работа, совершаемая над диэлектриком. В соответствии с граничным условием () имеем:

В соответствии с этой формулой имеем:

(3.12)

– элемент поверхности, 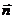– нормаль, внешняя по отношению к диэлектрику, т.е. внутренняя по отношению к проводнику. Индекс (1), относящийся к диэлектрику опущен, – заряд, сосредоточенный на поверхности проводника. Исходя из (3.12), имеем:

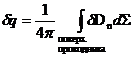
На поверхности проводника потенциал 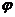постоянен, так что

Используя теорему Гаусса, получим

Здесь под диэлектриком понимается наш диэлектрик + вакуум. Пусть сторонних зарядов в диэлектрике не, т.е. незаряженный диэлектрик помещен в поле (проводника, который заряжен), и в этом поле он поляризуется и сам влияет на это поле. Тогда (см.(3.10)), а отсюда . Поэтому имеем далее:

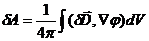
(3.13)

Здесь и – характеристики поля внутри диэлектрика. Интегрирование идет по всей области пространства, в том числе и по вакууму. В область интегрирования не надо включать область, занимаемую проводниками, хотя это и неважно, т.к. внутри проводников.

Итак, (3.11) можно записать в виде:

(3.14)

Можно ввести свободную энергию , тогда

(3.15)

Как уже отмечалось, (3.14) удобнее использовать в теплоизолированной системе (адиабатический процесс), (3.15) имеет смысл вводить при лишь постоянной вдоль всего тела температуре.

Фигурирующие в (3.14),(3.15.) величины относятся ко всему телу в целом, это не локальные характеристики. Как известно, локальные характеристики для каждого достаточно малого, но макроскопического участка тела свои, т.е. их можно рассматривать как функции координат тела.

Получим соотношения аналогичные (3.14) и (3.15) для единицы объема тела. Это означает, что внутри тела мы выделяем некоторый определенный объем и рассматриваем вещество в этом объеме. При этом число частиц в выделенном объеме переменно за счет обмена ими с окружением. Тогда наряду с энтропией или температурой появится новая независимая переменная число N частиц (пока электрическое поле во внимание не принимается)

Тогда можно записать:

где 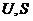– внутренняя энергия и энтропия единицы объема, – химический потенциал, отнесенный к одной частице.

Введем плотность массы вещества . Тогда, если - масса молекулы, – число частиц в выделенной единице объема, то 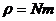.Отсюда

Здесь есть химический потенциал, отнесенный к единице массы. Таким образом, можно записать

(3.16)

Аналогично,

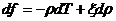
(3.17)

где – свободная энергия, приходящаяся на единицу объема. Оба этих соотношения имеют общий смысл и получены независимо от нашей задачи (разумеется, если бы мы вздумали получить подобное соотношение для единицы массы, то, в силу фиксированности количества вещества, мы бы имели фиксированное число частиц и вторых слагаемых справа в (3.16) и (3.17) не было бы).

Учтем теперь работу электрического поля над единицей объема вещества. Тогда будем иметь в соответствии с (3.14) и (3.16).

(3.18)

и в соответствии с (3.15), (3.17)

	(3.19)

(3.18), (3.19) справедливы не только для состояний истинного, но и для состояний локального равновесия. В последнем случае может меняться от точки к точке, так что и , и есть функции . Подчеркнем еще раз, что (3.18) есть (3.14), но записанное для единицы объема.

Наряду с и можно ввести термодинамические потенциалы соответственно по отношению к переменным и :

	(3.20)
	(3.21)

*) Для интегральных характеристик имеем соответственно

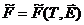
Тогда

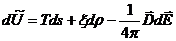
	(3.22)
	(3.23)

Осюда, в частности, имеем

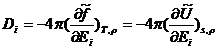
(3.24)

Поскольку

,

то

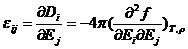
(3.25)

вследствие чего

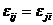
(3.26)

Запишем , 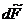через источники поля (т.е. через заряды на поверхностях проводников, создающих поле в диэлектрике). Заметим в начале, что (3.14) через потенциалы 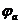на поверхности проводников и заряды записываются в виде

(3.27)

– дополнительный заряд, вносимый на проводник номера . Используем (3.14) и (3.20) для получения через источники поля.

Имеем

Займемся интегралом в правой части

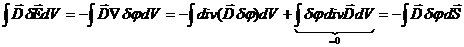
Здесь интегрирование идет по объему, закрытому данным диэлектриком + вакуум. В объеме диэлектрика (и вакуума) . Интеграл по поверхности есть интеграл на бесконечности и по границам проводников, создающих поле в диэлектрике. На бесконечности . Поэтому имеем далее:

На поверхности проводников потенциалы постоянны, т.е. 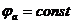. Здесь – не вариация, а добавка к потенциалу. Поэтому (но другая). Отсюда можно вынести за знак интеграла. Так как направлен вне диэлектрика, т.е. во внутрь проводника, а направлен во внутрь диэлектрика (см.(2.15)), то имеем:

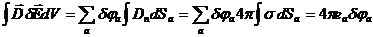
Таким образом

(3.28)

Если в (3.27) , то в (3.28)

Для свободной энергии имеем

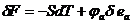
	(3.29)
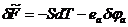
	(3.30)

Как известно из термодинамики, различные термодинамические потенциалы обладают свойством достигать в состоянии теплового равновесия минимума по отношению к различным изменениям состояния тела. При записи условий равновесий в электростатическом поле необходимо указывать, рассматриваются ли изменения состояния при неизменных зарядах или потенциалах проводников – источников поля. Так, 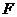или имеют в равновесии минимум по отношению к изменениям состояния, происходящих при и, соответственно, при постоянных зарядах или потенциалах проводников соответственно.

Если в теле могут происходить какие – либо процессы, не имеющие прямого отношения к электростатическому полю, например, химические реакции, то условия равновесия по отношению к этим процессам даются минимумом при заданной плотности и температуре тела и индукции вне, или минимумом при постоянной плотности, температуре и напряженности поля .

Полученные термодинамические соотношения справедливы при любой зависимости от . Рассмотрим теперь случай изотропного диэлектрика с линейной зависимостью . В этом случае основное термодинамическое соотношение можно проинтегрировать. Рассмотрим с этой целью локальные характеристики, в частности . Имеем

Диэлектрическая проницаемость есть функция состояния. Она зависит от энтропии , плотности , которые в принципе могут зависеть от координат. В случае изотропного и однородного диэлектрика зависимости и от координат нет. Следует также отметить, что не зависит от характеристик поля. Это связано с тем, что мы имеем линейную теорию. Итак, в случае изотропного диэлектрика (3.18) можно записать

Введем – локальную внутреннюю энергию в отсутствии поля (или ) тогда интегрируя (3.18”) получим

(3.31)

Аналогично

(3.32)

В соответствии с этими формулами могут быть записаны выражения для модифицированных локальных характеристик (см.(3.20), (3.21)).

	(3.33)
	(3.34)

Используя эти формулы, можно получить формулы для плотности энтропии и химического потенциала вещества. Так

(3.35)

Величина - химический потенциал в отсутствие поля. Таким образом, зависит от Е через квадратичную по Е добавку к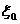

Не нашли, что искали? Воспользуйтесь поиском: