Мультипольные моменты.

В соответствии с изложенным в §3, можно утверждать, что потенциал 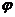, создаваемый системой зарядов в удаленной точке может быть представлен в виде разложения

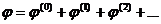
(4.31)

по степеням 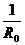; член 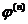в этом разложении пропорционален 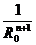. Мы видим, что первый член, определяется суммой всех зарядов, второй, 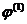называется дипольным потенциалом системы и определяется дипольным моментом .

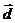Третий член разложения равен

(4.32)

где сумма по всем зарядам, индекс а, указывающий номер заряда, мы здесь опустим; 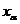компоненты вектора (т. е. ), а и 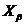- вектора .

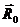Эта часть потенциала обычно называется квадрупольным потенциалом. Если сумма зарядов и дипольный момент системы равен нулю, то разложение начинается с .

В (4.32) входят шесть величин 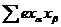. Легко, однако, видеть, что в действительности поле зависит не от шести независимых величин, а только от пяти. Это следует из того, что функция 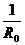удовлетворяет в соответствии с (4.11) уравнению Лапласа 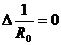. Это равенство можно записать в виде . Поэтому (4.32) можно написать в виде

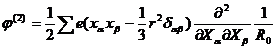
Тензор

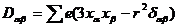
(4.33)

называется квадрупольным моментом системы. Из определения (4.33) следует, что сумма диагональных элементов этого момента равна нулю.

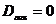
(4.34)

Симметричный тензор поэтому имеет всего пять независимых компонент. С его помощью можно написать

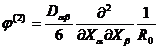
(4.35)

Производя дифференцирование

,

и учитывая, что

имеем в соответствии с (4.35)

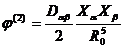
(4.35’)

или

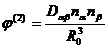
(4.36)

где 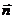- единичный вектор в направлении .

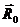Как и всякий симметричный тензор второго ранга, тензор может быть приведен к главным осям. При этом, в силу (4.34) два из главных значения этого тензора независимы.

Если же система зарядов симметрично относительно некоторой оси (ось Z), то она же является одной из главных осей тензора ; положение двух других осей в плоскости ху произвольно и все три главных значения связаны между собой

(4.37)

Обозначим компоненту 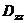через D. Ее называют обычно квадрупольным моментом. Запишем потенциал в этом случае. В соответствии с (4.36) имеем

(4.38)

где угол между 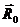и осью Z, а 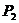- полином Лежандра.

Легко убедиться также в том, что квадрупольный момент не зависит от выбора начала координат, если равны нулю как полный заряд, так и дипольный момент системы.

Аналогичным образом можно было бы написать в (4.31) следующие члены разложения и определить так называемые мультипольные потенциалы и моменты.

Не нашли, что искали? Воспользуйтесь поиском: