
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Добавлю некоторые объяснения в пунктах алгоритма.
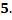 Когда я буду выносить выражение из-под корня, я обязательно подумаю, ставить мне модуль, или нет?
Когда я буду выносить выражение из-под корня, я обязательно подумаю, ставить мне модуль, или нет?
Надеюсь, примеры для этого пункта Вы подберёте себе сами, я же напомню о том, что в некоторых случаях Вам придётся раскрывать модуль. Тогда Вам понадобится метод раскрытия модуля.
Пример:
… = 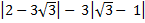 = …
= …
Обратим внимание, выражение в первом модуле – имеет отрицательное значение, тогда
заменим модуль скобками, а так же изменим знак перед модулем - на противоположный.
Выражение внутри вторых скобок, имеет положительный результат, тогда модуль опустим,
и вместо него поставим обычные скобки.
= 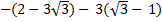 = – 2 +
= – 2 + 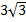 –
– 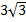 + 3 = 1
+ 3 = 1
-------------------------------------------------------
6. В примерах я могу пользоваться формулами сокращённого умноження.
Для этого пункта рассматриваются примеры некоторых формул:
α – ϐ = 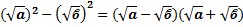 ; α =
; α = 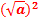
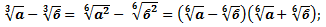
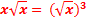
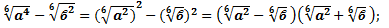
А также задание такого типа:
Решить. 
Покажем, как раскладывается формула под корнем 4-ой степени:
α 2 + 2 α b + b2 = ( α + b)2
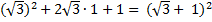 подставлять под формулу
подставлять под формулу
начнём с середины,
3+1 = 4 конкретно с цифры 2.
Тогда вместо буквы α будет  , а вместо буквы b – 1.
, а вместо буквы b – 1.
Проверим края и соберём формулу.
Далее можно продолжать запись решения:
… = 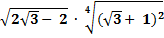 =
= 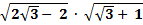 =
=
= 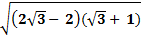 =
= 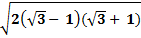 =
=  = 2
= 2
----------------------------------------------------------------------
В старших классах есть тема «Степенные функции с рациональными показателями.
Когда ученики имеют дополнительный материал под рукой, и знают, как им пользоваться, они потихоньку начинают работать.
 Чтоб запомнить, как построить график, можно воспользоваться таблицей:
Чтоб запомнить, как построить график, можно воспользоваться таблицей:
Но в учебнике такой таблицы нет, тогда, разбирайся сам…
Многие говорят: «Пока я разберусь, что к чему, изучение темы уже закончится, а оценок плохих я уже нахватал. Тематическая оценка хорошей не будет, и потом, где оно мне понадобится?»
В некотором смысле ученик действительно прав. Помогите ему, дайте яркий, удобный, легко воспринимаемый материал, для изучения. У Вас при этом увеличится процент высоких оценок.
Согласитесь с тем, что в наше время льётся не информационный дождь, а сильный ливень информации. Много чего хочется узнать, многому научиться, но информация школьного учебника, абсолютно детей не привлекает. Она, настолько бедна в подаче материала, что при современных эффектах компьютерной технологии, мы должны понять, почему ученики не только не учат учебник, а даже глянуть на него не хотят.
Нам ещё никто не отменял разрешение выбирать самому метод ведения урока, значит, есть возможность поменять старые не интересные занятия, на лучшие, новые, завлекающие, идущие в ногу со временем и удобные для пользования. Понятно, что на это уйдёт много времени, и сил, но это того стоит. Вы будете лучшим, продвинутым, любимым и уважаемым для учеников, что в наше время бывает очень редко.
Вирус 21-го века – «провал памяти»
Играть с детьми на занятиях, это понятие разное. Для некоторых нужна серьёзная подготовка, вспомогательные материалы, и много чего.
Но бывают случаи, когда само занятие вдруг превращается в игру без какой-либо подготовки. Вы абсолютно не думали готовиться, собирать дидактический материал, учить сценарий. Само собой во время проведения занятия, пришла шуточная идея, и пошутив, Вы поняли, как изменился ход урока. Все шутили, смеялись, в конце вы подвели итог, и всё это превратилось в игру.
Не хочу обижать многих преподавателей, но такие изменения на уроке или занятии, может допустить не каждый, и это плохо. Легко стукнуть кулаком по столу и сказать: «Всё! Тихо! Продолжаем занятие!» Но это не всегда действует и постоянство такого поведения преподавателя, приводит к упадку настроения учеников.
Опытный профессионал поступит по-другому. Он выстроит всё положение так, как выгодно ему, но и дети останутся довольны и с отличным настроением. Если каждое Ваше занятие имеет какую-то новую изюминку, интригу, игру, представление, Вы станете «Центром притяжения». На Ваши занятия ученики пойдут с интересом, с желанием, и не одни. Они поведут за собой своих друзей и всем расскажут о своём не похожим на всех, сказочном учителе – репетиторе, занятия которого превращаются в сказку.
Именно о таком переходе из стандартного занятия в игровое, мне и хочется рассказать.
Всем известно, что домашняя работа и повторение закрепляет выученный материал, но мы знаем, как часто ученики не выполняют наши задания без нас. Это приводит их к ошибкам, а нас нервирует.
Мы чётко помним, как на прошлом занятии исправляли эту же ошибку, и снова она оказалась в тетради. Мы заново работаем с этой ошибкой, но кто уверен, что на следующем занятии, она исчезнет? Вы уверены, что ученик каждый раз слушает Вас, а не думает о своём?
Какой вывод? Надо зацепить внимание ученика каким-то образом.
Но это стандартный урок – занятие, для которого Вы не готовили что-то особенное, никаких дидактических материалов и всего такого, что поможет привлечь интерес ребёнка. Здесь может сработать только Ваша фантазия.
Например, Вы - врач.
Любая ошибка ученика, это шуточная «болезнь», которую надо вылечить: ОРЗ; простуда; кашель; насморк; головная боль; свинка; ушиб…
Я думаю, много разных «болезней» для излечения ошибок, можно придумать. Каждая ошибка имеет свой диагноз и своё лечение. Для этого вы можете дать рецепт и направить ученика лечиться.
Рецепт. Это тот материал, который надо знать для исправления ошибки.
Лечение. Заставить ученика выучить этот материал сейчас на занятии. Возможно, ему понадобится переписать в тетрадь этот материал, чтобы он был рядом. Далее дать задание, в котором предполагается возможность совершить такую же ошибку, и показать правильность действия выписанного «лекарства».
Обязательно записать в тетрадь название ошибки или темы и её поставленный диагноз, а также коротко описать лечение. Это должен сделать сам ученик.
Этому ученику в дополнении к общей домашней работе, обязательно дать «лекарство» от болезни – ошибки и «процедуры для излечения» - пару похожих заданий с такими ошибками.
Такое занятие ни чем не отличается от стандартного, но само введение в него игрового смысла, поднимает настроение и интерес детей. Им становится весело, они смеются и при этом «лечатся».
Также, по этому сценарию, можно провести игру на тему: «Вылечим наши ошибки». Для такой игры Вам понадобятся уже напечатанные рецепты – правила, которые можно будет раздавать учащимся для лечения поставленного диагноза. А также дополнительные процедуры для лучшего и быстрого лечения. Это могут быть карточки с такими же ошибками, которые надо найти и исправить, или мини задания, при выполнении которых учитывается знание материала связанного с такой ошибкой. Можно дать просто пример, похожий на тот, в котором ошибка допущена.
Всё зависит от того, как Вы подготовитесь к «лечению заболеваний» этой темы. Конечно, надо не упустить ошибки прошлых тем, которые могут быть допущены на этом занятии. По этому, если Вы решили первый раз попробовать такую игру, внимательно продумайте, какие задания можно давать на этом уроке, и какие ошибки при этом могут быть допущены Вашими учениками?
Если усложнить игру, то ошибки можно разделить на сложные болезни и лёгкие, на постоянные и редкие. Возможно предложение - в домашней работе найти лечение с помощью «Рецептов моей бабушки». Конечно, сюда необходимо будет привлечь родителей, но это иногда очень хорошо помогает.
А также предложить найти свой рецепт. Свои рецепты учащимся находить не хочется, хотя бывают исключения. Такой случай необходимо отмечать, как особый метод самоизлечения. Для таких детей у меня всегда есть мини подарки.
Если мы идём в ногу со временем, мы начнём понимать учеников и помогать им устойчиво стоять, хорошо ориентируясь на этой земле.
Свободу хакеру – Мише!
Каждый ученик – индивидуум. Работая с ними и присматриваясь к ним, я поняла, ведь с их помощью можно придумывать и рассматривать всё новые и новые методы обучения. Своим непониманием и забывчивостью, ученики сами подсказывают шаги решения того или иного вопроса.
Был у меня один ученик 6-го класса. Придёт на занятие, решаем уравнения, разберём ошибки, выучим правила, всё ему понятно. Объяснение проводилось по сказочному сценарию, чтоб было желание работать. Уходит домой с домашней работой без вопросов. На следующем занятии, приносит домашнюю работу с ошибками, и всё повторяется снова. Заколдованный круг получается. Что делать?
Присмотрелась я к нему, поговорила о том, о сём, уж очень он себялюбивым оказался. Ну, думаю, какой подход найти к решению этих уравнений?
Пришёл он на следующее занятие, снова неизвестное - х найти не может, и тут меня осенило…
Миша! Ты хакер с позывным – Х (икс). Тебя украли и держат в подземелье. Тебе надо себя освободить.
| уловие: – 2(х + 3) + 4(х – 2) = 5 решение карта подземелья – 2(х + 3) + 4(х – 2) = 5 кабинет главаря камеры коридор |
План освобождения:
1. Осмотреть карту подземелья;
2. Предполагаемые камеры, в которых ты можешь находиться, раскрываются, если к ним внутрь кто-то заходит. Потому, в течение дня, их обязательно надо раскрыть;
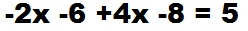
3. Далее надо разобраться, сколько охранников ХОДЯТ рядом с тобой, и сколько подставных кротов ПРИЛИПЛИ к тебе, для выяснения особой информации.
Охранники ходячие – слагаемые, кроты прилипшие – множители;

4. Ходячих охранников отправляем к главарю с отчётом, меняя при этом знаки;
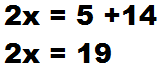
5. Если всё идёт по плану, то прилипших кротов главарь сокращает сам, ведь они не смогли достать нужную информацию;
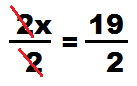
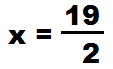 6. Когда ты остаёшься один, - ты свободен!!!
6. Когда ты остаёшься один, - ты свободен!!!
Свобода хакеру Мише!!!
После этого метода, я перестала снова и снова проводить объяснения, достаточно было сказать, что он должен освободить себя, и Миша начинал самостоятельно вспоминать, как это делается.
В выполнении действий при раскрытии скобок и сложении подобных слагаемых, ошибок не было, по этому, я не концентрировала на это внимание.
Этот же метод решения я начала предлагать другим ученикам, с другими именами, ученикам нравилось, метод действует!
Вы Гарри Потера знаете?
Естественно, - скажете Вы. Кто о нём не знает?
А почему о нём все так быстро узнали? Ответ очевиден. Он очень интересный сказочный герой. Книга Джоан Роулинг написана для читателей всех возрастов, смысл ясен и понятен, а содержание такое, о чём ещё никто и никогда не писал.
Ну, с этой книгой всё понятно. А вот математика у нас – царица всех наук, но для детей, почему-то ясно написать не очень получается.
Все считают, что учебник по математике – это обучающая наука, а не игра для учащихся. Дети с удовольствием учат то, что их интересует, а все остальные знания даются «из-под палки». Так почему бы нам не помочь Царице -Математике стать интересной, сказочной, а может и фантастической для наших учеников.
 Для этого можно придумать одного, а может и несколько сказочных героев, которые учат математику, как фиксики – физику, например.
Для этого можно придумать одного, а может и несколько сказочных героев, которые учат математику, как фиксики – физику, например.
 Воспользуйтесь своей фантазией и придумайте такого героя, как у меня, Чёртик по имени Крутик, который в 6-ом классе играет с детьми во все игры, рассказывает о своих интригах в брошюре и показывает свои похождения в презентациях.
Воспользуйтесь своей фантазией и придумайте такого героя, как у меня, Чёртик по имени Крутик, который в 6-ом классе играет с детьми во все игры, рассказывает о своих интригах в брошюре и показывает свои похождения в презентациях.
В видеороликах моим напарником стал маленький шут по имени Носик. Мои ученики очень любят этих героев. В геометрии 7-го класса, теоретическую часть им объясняет угол с весёлым именем Кутик.
Чем интересней и загадочней будет ваш герой, тем больше детского внимания привлечёт он к себе. Тем проще станет сложное объяснение учебного материала, и веселее будут проходить обыденные занятия.
 Стереометрия – расположение прямых и плоскостей в пространстве.
Стереометрия – расположение прямых и плоскостей в пространстве.
Когда в школьной программе учащиеся начинают изучать стереометрию, хорошо, если в школе есть предмет – черчение. Бывает, во многих школах вести его некому, тогда изучение стереометрии в течение двух лет, приходит к плачевному результату. Что делать в таком случае?
Научить детей пользоваться вспомогательными материалами на уроках стереометрии. Что это за материалы?
1. Стол – основная плоскость;
 2. Ручки – прямые и отрезки;
2. Ручки – прямые и отрезки;
3. Резинки – стирки – точки;
4. Каждая тетрадь – новая плоскость;
5. Раскрытая тетрадь – пересечение двух плоскостей.
 С помощью этих вспомогательных материалов можно представить реальную картину правил и увидеть построение воочию, чего не хватает ученикам в этих случаях. Действительно, без вспомогательных материалов наши ученики не представляют, где находится угол между плоскостями, сколько прямых в пространстве не могут пресечь плоскость, и многие другие вопросы.
С помощью этих вспомогательных материалов можно представить реальную картину правил и увидеть построение воочию, чего не хватает ученикам в этих случаях. Действительно, без вспомогательных материалов наши ученики не представляют, где находится угол между плоскостями, сколько прямых в пространстве не могут пресечь плоскость, и многие другие вопросы.
 Для этого на своих занятиях репетитор должен научить создавать стереометрическую картинку, как говорится, «из ничего».
Для этого на своих занятиях репетитор должен научить создавать стереометрическую картинку, как говорится, «из ничего».
Первоначально для осмотра, можно использовать наглядное пособие, а затем ученики попробуют сами сделать такую фигуру со своего вспомогательного материала в любом месте, в школе или дома. В дальнейшем на уроках, при решении различных задач, такие навыки помогают выполнить правильное построение рисунка условия, а также разобрать все свойства фигуры, воспроизведённые при построении, и решить задачу.
В некоторых случаях, приходится на занятии с помощью бумаги и ножниц восстанавливать настоящую фигуру, описываемую в условии, но это бывает редко.
Стереометрия – сечения.
Мы говорили о необходимости преподавания в школе предмета «Черчение», особенно его знания нужны в начале 10-го класса в теме «Сечения» по геометрии.
Построить сечение стереометрической фигуры не так просто, как кажется. Требуется видеть или представлять не только внешнюю часть данной фигуры, но и внутреннюю, особенно учитывать искажения, происходящие со стереометрическими фигурами на плоскости. Очень редко всё вышесказанное мной, может иметь наш ученик. С чего начать в этом случае подготовку данной темы и как объединить все пробелы в эффективный метод обучения? На этот вопрос постараюсь ответить, и показать, как это делаю я
Всю практическую подготовку этой темы можно разделить на три этапа изучения.
1. На первом этапе ученики учатся соединять точки, принадлежащие только одной плоскости. К сожалению, есть такие ученики, которым и это не под силу. Если Вы думаете, что никакая помощь в этих действиях не требуется, Вы сильно ошибаетесь.
На этом этапе, ученики учатся видеть планиметрическую фигуру, на сторонах которой расположены точки, которые надо соединять. Так же с особой точностью карандашом пробуют визуально обводить эту грань, при этом называя все её вершины.

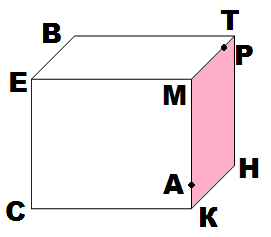
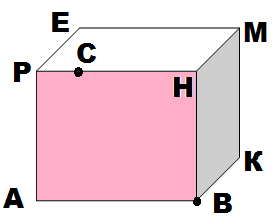
В следующих заданиях можно использовать три, четыре, пять точек уже находящихся на рёбрах фигуры. Цель – выполнить правильное соединение всех точек и получить сечение.
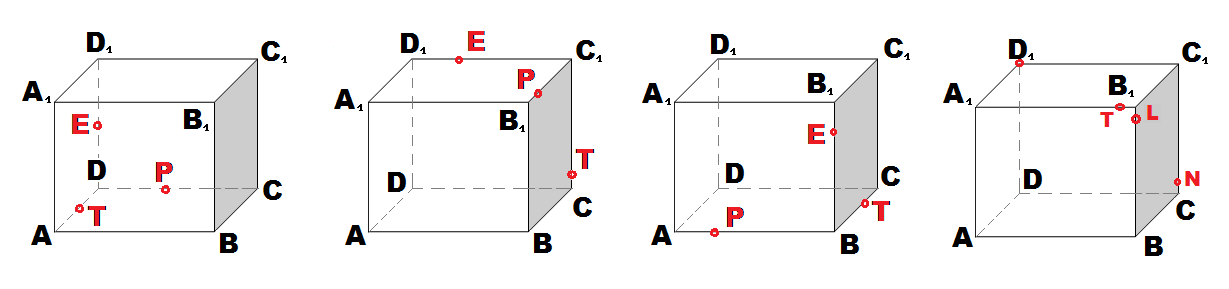 Для многих учеников такие действия не доставят труда, поэтому к условиям построения этих задач, можно добавить доказательство полученной фигуры, или вычисление площади найденного и построенного сечения.
Для многих учеников такие действия не доставят труда, поэтому к условиям построения этих задач, можно добавить доказательство полученной фигуры, или вычисление площади найденного и построенного сечения.
Как бы ни было, уделите внимание детям, не видящим граней многогранника с нужными для соединения точками. Это понадобится для работы на следующих этапах. Такие ученики проявят себя, неумением правильно читать и видеть название грани, на которой можно соединить две точки.
Хотелось бы, на этом этапе, иметь необходимые задачи с рисунками, но их в учебниках нет. Тогда сделайте себе и распечатайте достаточное количество карточек, показанных выше, это ускорит изучение данного этапа.
2. Второй этап в построении сечения «методом следов», достигается у каждого по-разному, но в конце, ошибок почти не бывает.
Какие действия мы учим на втором этапе?
Учимся проводить прямую, соединяющую две точки, и находить следы пересечения этой прямой с продолжениями сторон грани.
Это действие является сложным, пока грань находится в стереометрической фигуре. Как только мы делаем дополнительный чертёж этой грани, перечерчивая её отдельно от фигуры, и продлеваем далее все четыре её стороны, видимость пересечения этих сторон с прямой, становится очевидной.
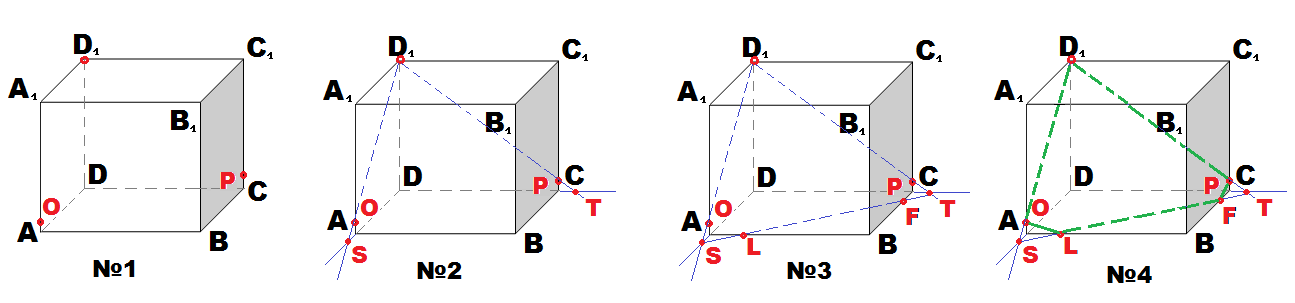 Понимая происходящие действия, учащиеся, перестают ошибаться, и осмысленно находят нужные «следы» на сторонах этой грани.
Понимая происходящие действия, учащиеся, перестают ошибаться, и осмысленно находят нужные «следы» на сторонах этой грани.
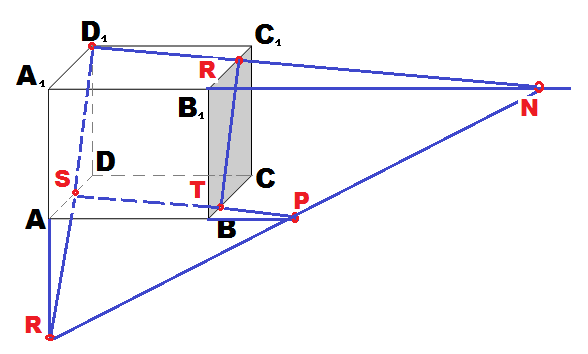
Рассмотрим пошаговое построение сечения на четырёх рисунках.
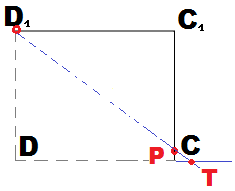
Рисунок №1. Условие: построить сечение параллелепипеда, плоскостью, которая проходит через точки D1 ,O,P.
 Рисунок №2. Для соединения точек D1 и O прямой, а также нахождения точки – «следа», нарисуем дополнительный чертёж грани АА1DD1 в таком виде, в каком она искажена
Рисунок №2. Для соединения точек D1 и O прямой, а также нахождения точки – «следа», нарисуем дополнительный чертёж грани АА1DD1 в таком виде, в каком она искажена
на рис. №2.
Затем, продлевая все стороны грани, можно увидеть, с продолжением какой стороны пересекается прямая D1 O.
Осмотрев свой дополнительный чертёж, ученик не выполнит пересечение прямых D1 O, и АВ на общем рисунке.
 Далее аналогично строятся и рассматриваются плоскости граней: DD1 С1 С и АВСD.
Далее аналогично строятся и рассматриваются плоскости граней: DD1 С1 С и АВСD.
Все выполненные дополнительные чертежи переносятся на основные рисунки №2 и №3.
Рисунок №4 напоминает действия первого этапа, в котором сечение ОD1 PFL легко построить, при имении всех необходимых точек сечения.
---------------------------------------------
 Первоначально, на данном этапе, проблема только в построении дополнительного чертежа. Дети не очень хотят перерисовывать стороны отдельно, они не видят в этом необходимости. Зачастую, приходится рисовать два, три, а то и четыре чертежа, это их сильно напрягает. Не идите у них на поводу, стойте на своём и заставьте выполнить как надо, все шаги действия. В крайнем случае, дайте ученику шанс решать самостоятельно, но до первой ошибки. Потом Вам легче станет управлять им.
Первоначально, на данном этапе, проблема только в построении дополнительного чертежа. Дети не очень хотят перерисовывать стороны отдельно, они не видят в этом необходимости. Зачастую, приходится рисовать два, три, а то и четыре чертежа, это их сильно напрягает. Не идите у них на поводу, стойте на своём и заставьте выполнить как надо, все шаги действия. В крайнем случае, дайте ученику шанс решать самостоятельно, но до первой ошибки. Потом Вам легче станет управлять им.
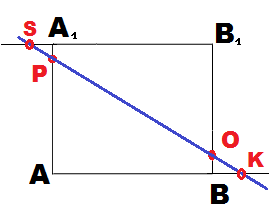 3. Третий этап сложен только в том, что появляются лишние «следы» пересечения, прямой и сторон грани, мешающие увидеть нужные точки для продолжения решения.
3. Третий этап сложен только в том, что появляются лишние «следы» пересечения, прямой и сторон грани, мешающие увидеть нужные точки для продолжения решения.
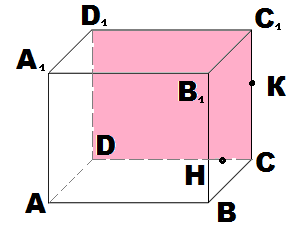
Например, в условии рисунка слева, на грани AA1B1B находятся две точки Р и О. Проведя через них прямую линию, на дополнительном чертеже, появляются также две точки пересечения прямой со сторонами прямоугольника. Иногда в дальнейшем решении используются обе полученные точки S и K, а иногда приходится выбирать, какая нужна, а какая нет. Но решив несколько задач, учащиеся начинают понимать, какую часть дополнительного чертежа можно и нужно использовать.
 При таком методе построения сечений, количество ошибок уменьшается всего до 5-7 %. Даже тугодумы пристраиваются к выполнению стандартных действий, и считают, что эта тема – одна из самых лёгких.
При таком методе построения сечений, количество ошибок уменьшается всего до 5-7 %. Даже тугодумы пристраиваются к выполнению стандартных действий, и считают, что эта тема – одна из самых лёгких.
Не нашли, что искали? Воспользуйтесь поиском: