
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Мои любимые пятиминутки
Всё интересное, весёлое, яркое, запоминается, можно сказать – «хорошо». О постоянном повторении мы говорили тоже. Интересная система зачётов, игр, это всё отлично, но бывают такие моменты, когда по какой-то причине, нет сил «играть». В это время мы понимаем, что обычный школьный урок репетитору проводить будто бы не положено, а на что-то другое, сил нет. В такой момент могут прийти на помощь пятиминутки.
Репетиторские пятиминутки немного отличаются от школьных. Пятиминутный проверочный математический диктант в школе проводится для проверки знаний и выставления оценок. Я пользовалась этим методом, когда тема была сложной, и в журнале действительно, не хватало оценок, проводила при этом пятиминутный мини-диктант.
Я ещё тогда обратила внимание, что необходимость проверки ошибок сразу после диктанта, себя оправдывает. Дети концентрируют внимание на задания этой пятиминутки, стараются написать верные ответы, при этом они заставляют свой мозг работать, и тут же, не успев расслабиться, горят желанием узнать результат. И представьте себе, ученики сдают свои листочки с работой учителю, но разбирая задания на доске, помнят свой ответ, при этом радуясь или жалея.
То есть, пока они готовы работать, мы даём им такую возможность, показав какие ошибки при этом могут быть. Это вы можете сделать в начале занятия с группой. После разбора ошибок, можно перейти к обычной работе Вашего занятия, но не до конца. Почти за пять минут до окончания, вы повторите свою пятиминутку снова, поменяв местами бывшие задания. Соберёте листочки, и увидите разницу ответов в начале и в конце. Когда такие пятиминутки будут повторяться, дети чётко будут знать, что вникать в разборку ответов надо с ещё большим вниманием, чтоб потом, написать своё решение без ошибок. Таким образом, два раза с помощью маленьких пятиминуток, Вы «поднимите адреналин» своих учеников для изучения некоторых основных правил, или решения некоторых заданий.
Вы можете придумать какое-то поощрение за правильные ответы, ведь оценки репетитор не ставит. В любом случае занятие будет продуктивным и не требующим от Вас больших усилий.
 Как ученикам понять тригонометрию?
Как ученикам понять тригонометрию?
Тригонометрия считается очень сложным разделом алгебры. Почему?
Это самый большой раздел, который разбит на пять основных частей данной темы. Раньше тригонометрия – это был отдельный предмет, который изучался два года в старших классах. Сейчас его сжали, решили, что не такой уж он и сложный, и возложили всё его изучение за короткий срок на учителей и репетиторов. По этому, берём себя в руки и начинаем готовиться к тому, как усовершенствовать этот раздел, чтоб всем ученикам было легче.
Разделим всю тригонометрию на 7 частей. Семь – это хорошее число в математике, поэтому, настраиваемся на лучшее.
1. Начало (введение).
2. Формулы.
3. Функции.
4. Примеры.
5. Уравнения.
6. Неравенства.
7. Системы уравнений.
Попробую по каждой части в поделиться некоторыми своими наработками.
Начало (введение).
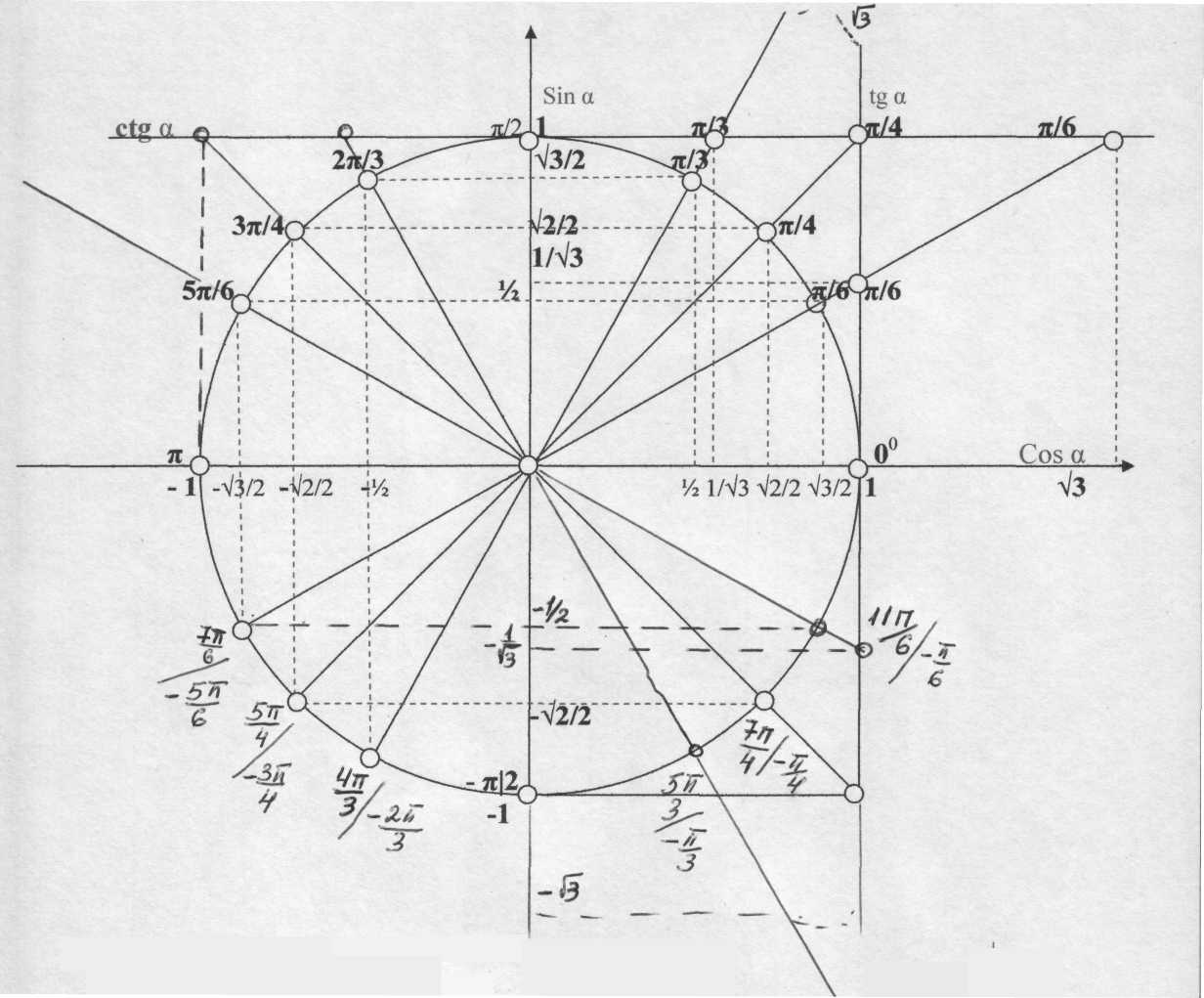
На первом уроке, можно коротко, на основе геометрии показать, зависимость величины угла от сторон в прямоугольном треугольнике. Также ознакомить с нахождениями синусов и косинусов различных углов от 00 до 3600.
| В |
| О |
| М |
| Е |
| D |
| A |
| C |
| α |
| R |
 Далее объяснив ученикам, что обозначает знак -
Далее объяснив ученикам, что обозначает знак -  на единичной окружности, выясняется, какая часть от величины
на единичной окружности, выясняется, какая часть от величины  , принадлежит углу 300.
, принадлежит углу 300.
Потом, всё просто. Вместе с учениками, начните просчитывать величину следующего угла:
600 = 300 + 300 =  ,
,
затем следующего, и так до угла 2400. Все остальные просчёты до 3600, дать домой. В оставшееся время, находить по данным углам только значения их синусов и косинусов.
На втором уроке ещё раз повторить всё, что изучалось на первом, и ввести нахождение значений тангенсов и котангенсов всех углов на единичной окружности.
Затем можно показать формулы перехода от градусной меры в радианную, и наоборот.
В первой части - изучение единичной окружности, является путевой звездой всей темы тригонометрия. К её изучению надо подойти очень серьёзно.
Далее уже готовую единичную окружность для пользования, нужно иметь в своём мини справочнике.
Формулы.
Формулы в моей брошюре, разделены на два листа. На первом расположены те, которыми должны уметь пользоваться все ученики.
На втором листе располагаются те формулы, которые используются редко, но необходимы ученику для углублённого изучения математики.
Все формулы на двух листах разделены по группам, их так удобно учить.
Первая группа состоит из основных формул, в которую входят одинаковые углы. В этой группе формулы удобно учить, не выговаривая названия углов.
Пример: синус в квадрате, плюс косинус в квадрате, равно единице.
В таком же виде учатся и остальные формулы, это удобно и лучше запоминается. Если Вы думаете, что ученики потом начнут писать примеры без углов, это не правда. Главное, дать понять, что функция sin, или cos без углов не существует, и между углом и названием функции, не может быть просвета, или знака умножения, то есть, угол – это внутренность самой функции.
Объяснив таким образом, что есть что, Вы избежите многих ошибок и облегчите изучение самых сложных формул алгебры.
Не нашли, что искали? Воспользуйтесь поиском: