Основные тригонометрические формулы.

----------------------------------------------------

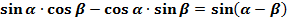
ІІІ. группа: Формулы двойного угла:

----------------------------------------------------

ІV. группа:

,

----------------------------------------------------

Формулы третьей группы удобней учить без конкретного названия углов. Это не совсем так, как формулы первой группы, но с особым подходом.

Пример: Синус двойного угла равен - два умножается на синус и косинус, углы пополам.

Первое впечатление, что эта фраза – полный абсурд, но учитывая то, что в примерах не всегда будет находиться угол 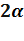, Вы чётко научите учеников делить любой двойной угол в этих формулах - пополам.

Самой сложной в этой группе, является запись трёх формул косинуса двойного угла.

Ученикам не ясно, зачем эта формула записывается в трёх видах, как её выучить, чтоб не путаться, и где какую применять?

Если вы ответите на эти три вопроса, все ошибки, связанные с использованием этих формул почти исчезнут.

1. Формула косинуса записана в трёх видах потому, что используется в разных примерах по-разному.

2. Её выучить очень просто, если за основу взять вид записи:

Сравнить её сходство и отличие с формулой: cos² x + sin² x = 1.

cos² x + sin² x = 1

А затем показать, что при уходе из записи , на её место становится единица, а синус в квадрате увеличивается в 2 раза. Такое же изменение происходит и с синусом в квадрате. После этого, ученики осмыслят запись трёх почти одинаковых (на взгляд) формул, и выучат их легко.

3. На вопрос: «Где какую формулу применять?» Ответ можно дать в четвёртой части, когда будут решаться примеры и использоваться алгоритм решения.

Но здесь, уходя вперёд, объясню.

Первая часть формулы часто используется в решении примеров, как формула сокращённого умножения:

Вторую и третью формулы, имеющие в слагаемом единицу, используют в примере, для сложения с другой единицей, которая мешает сокращению.

Допустим, имея такую дробь в условии , можно убрать единицу и выполнить сокращение:

С формулами второй и четвёртой группы, тоже можно поработать и подать их в удобном для запоминания виде.