Отношение делимости и его свойства. 1. Правило деления суммы на число

Правила деления

1. Правило деления суммы на число. Если частные натуральных чисел а и с, в и с существуют, то

(а + в): с = а: с + в: с.

Доказательство. Пусть q ₁ частное чисел а и с, q ₂ – частное чисел в и с, т.е. а = с · q ₁, в = с · q ₂, следовательно, а + в = cq ₁ + cq ₂ = c (q ₁ + q ₂). Последнее равенство означает, что частное получаемое при делении а + в на с, равно q ₁ + q ₂, т.е. а: с + в: с.

Примечание: а: (в + с) ≠ а: в + а: с.

Например, 66: (2 + 4) ≠ 66: 2 + 66: 4.

2. Правило деления разности на число. Если частные натуральных чисел а и с, в и с существуют и а ≥ в, то (а – в): с = а: с – в: с.

Доказательство этого правила аналогично доказательству правила деления суммы на число. (Читателю предлагается выполнить его самостоятельно).

П р и м е р. 192: 4 = (200 – 8): 4 = 200: 4 – 8: 4 = 50 – 2 = 48.

3. Правило деления произведения на число. Если существует частное чисел а и с, то (а · в): с = (а: с) · в. Если существует частное чисел в и с, то (а · в): с = (в: с) · а.

Доказательство. Пусть частное чисел а и с существует и равно х, тогда а = с · х, умножим обе части этого равенства на в, получим
а · в = с · х · в = с · (в · х) и потому (а · в): с = в · х = в · (а: с) = (а: с) · в.

П р и м е р. 560: 7 = (56 · 10): 7 = (56: 7) · 10 = 80.

4. Правило деления числа на произведение. а: (в · с) = (а: в): с =
= (а: с): в. Докажем, что а: (в · с) = (а: в): с. Обозначим а: (в · с) = t Þ а = (в · с) · t. а: в = ((в · с) · t): в = с · t. (а: в): с = (c · t): с = t.

П р и м е р. 480: 60 = 480: (6 · 10) = (480: 10): 6 = 48: 6 = 8.

В начальном курсе математики определение деления как операции обратной умножению в общем виде не дается, но постоянно используется. В начальных классах дается пояснение: деление связано с умножением. Разделить 48 на 4 – значит найти число, которое при умножении на 4 дает 48. Это число 12. Значит, 48: 4 = 12.

Деление с остатком

Рассмотрим пример из начального курса математики:

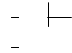7368 24

72 307

168

В этом примере пришлось 3 раза выполнять деление с остатком:

73: 24 = 3 (ост. 1);

16: 24 = 0 (ост. 16);

168: 24 = 7 (ост. 0).

С делением с остатком ученики знакомятся во втором классе на примерах: 11:2 = 5 (ост. 1), 19: 4 = 4 (ост. 3). Остаток при делении всегда должен быть меньше делителя.

Определение. Делением с остатком натурального числа а на натуральное число в называют правило, посредством которого находится пара натуральных чисел q – неполное частное и r – остаток, удовлетворяющих следующим условиям:

1) а = вq + r,

2) 0 ≤ r < в.

Теорема. Каковы бы ни были натуральные числа а и в частное q и остаток r при делении а на в всегда существуют и притом единственные.

Доказательство существования частного и остатка.

В случае, когда а делится на в, а: в = q (ост.0), значит, а = вq + 0, 0 ≤ 0 < в.

В случае, когда 0 < а < в и а не делится на в, а: в = 0 (ост. а), значит, а = в · 0 + а, 0 ≤ а < в.

В случае, когда а > в и а не делится на в (например.86: 10), для отыскания частного и остатка проведем следующие рассуждения. Рассмотрим возрастающую последовательность натуральных чисел, кратных в:

в · 1, в · 2, в · 3,..., в · q, в (q + 1), ….

Эта последовательность возрастающая, т.к. в ≥ 1. Нетрудно заметить, что число а расположится между двумя членами рассматриваемой последовательности, но ни с одним из членов последовательности совпадать не будет, т.к. по условию а не кратно в. Найдем наибольшее q, для которого в · q < a и в (q + 1) > а. Так как a > вq, то разность а – вq существует, т.е. а – вq = r, где r Î N ₀, т.к. в (q + 1) > а, то вq + в > а и в > а – вq, т.е. в > r. Мы доказали, что найденное r < в. Итак, для всех возможных случаев:

1) а = вq + r,

2) 0 ≤ r < в.

Паре (а, в) поставили в соответствие пару (q, r).

Докажем единственность частного и остатка.

Предположим, что для пары (а, в) существует 2 пары чисел: 2 частных и 2 остатка, для которых:

.

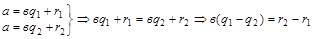Левая часть последнего равенства делится на в, значит и правая должна делиться на в, но r ₁ < в, r ₂ < в, значит r ₂ – r ₁ < в, отсюда
r ₂ – r ₁ = 0. Значит, r ₁ = r ₂ и q ₁ = q ₂. Единственность доказана.

Следствие. Если делимое и делитель при делении с остатком увеличить или уменьшить в одно и то же число раз, то частное не изменится, а остаток, соответственно, увеличится или уменьшится во столько же раз.

Действительно, пусть а: в = q (ост. r), тогда:

1) а = вq + r,

2) 0 ≤ r < в.

Умножим обе части 1) и 2) на т Î N, получим:

1) am = вqт + rт,

2) 0 ≤ rm < вm.

Отношение делимости и его свойства

Определение. Говорят, что число а делится на число в, если существует такое число c Î N₀, что а = в · с.

В том случае, когда а делится на в пишут: а в. Читают: «а делится на в»; «а кратно в»; «в – делитель а». Например, 12 делится на 6, так как существует такое с = 2, что 12 = 6 · 2, иначе 12 6.

Замечание. Записи 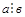и а: в не равносильны. Первое обозначает, что между числами а и в имеет место отношение делимости (возможно нацело число а разделить на число в). Второе – есть обозначение частного чисел а и в.

Отношение делимости обладает рядом свойств.

1°. Нуль делится на любое натуральное число, т.е.

(" в Î N) [0 в ].

Доказательство. 0 = в · 0для любого в, отсюда по определению следует, что 0 в.

2°. Ни одно натуральное число не делится на нуль, т.е.

(" а Î N) [ а 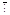0].

Доказательство (от противного). Пусть существует c Î N₀, такое, что а = 0· с, но по условию а ≠ 0,значит ни при каком с это равенство не выполняется. Значит, наше предположение о существовании с было неверным и а 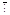0.

3°. Любое целое неотрицательное число делится на единицу, т.е.

(" а Î N) [ а 1].

Доказательство. а = 1· а => а 1.

4°. Любое натуральное число делится само на себя (рефлексивность), т.е.(" а Î N) [ а а ].

Доказательство. а = а · 1Þ а а.

5°. Делитель в данного натурального числа а не превышает этого числа, т.е. (а в Ù а > 0) Þ (а ≥ в).

Доказательство. Так как а в, то а = в · с, где c Î N ₀. Определим знак разности а – в. а – в = вс – в = в (с – 1),поскольку а > 0, то с ≥ 1, следовательно, в (с – 1) ≥ 0,значит а – в ≥ 0 Þ а ≥ в.

6°. Отношение делимости антисимметрично, т.е.

(" a, в Î N ₀)[(a в Ù в а) Þ а = в ].

Доказательство.

1 случай. Пусть а > 0, в > 0,тогда имеем:

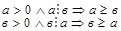(по свойству 5°). Значит, а = в.

2 случай. Пусть хотя бы одно из чисел а или в равно 0.

Пусть а = 0, то в = 0по 2°, т.к. иначе в не могло бы делиться на а. Значит а = в.

7 °. Отношение делимости транзитивно, т.е.

("a, в, с Î N ₀) [(a в Ù в с)Þ а с ].

Доказательство. а в Þ ($ к)[ а = вк ]; в с Þ ($ ℓ)[ в = cℓ ].

а = вк = (сℓ) к = с (ℓк), ℓк – произведение двух неотрицательных целых чисел ℓ и к и потому само является целым неотрицательным, т.е. а с.

8°. Если каждое из чисел а и в делится на с, то их сумма а + в делится на с, т.е. (" a, в, с Î N ₀)[(a с Ù в с) Þ (а + в) с ].

Доказательство, а с Þ а = ск, в с Þ в = cℓ.

а + в = ск + cℓ = с (к + ℓ), т.к. к + ℓ –целое неотрицательное число, значит (а + в) с.

Доказанное утверждение справедливо и в случае, когда число слагаемых больше двух.

Если каждое из чисел а ₁,..., а_п делится на с, то их сумма а ₁+... + а_п делится на с.

Кроме того, если числа а и в делятся на с, причем а ≥ в, то их разность а – в делится на с.

9°. Если число а делится на с, то произведение вида ах, где x Î N ₀, делится на с, т.е. а с Þ (" x Î N ₀)[ ax с ].

Доказательство. а с Þ а = ск, но тогда ах = скх = с (к · х), к,
x Î N ₀, значит ах с.

Следствие из 8°, 9°.

Если каждое из чисел а ₁, а ₂,..., а_п делится на с, то каковы бы ни были числа х ₁, х ₂, ..., х_n число а ₁ х ₁ + а ₂ х ₂ +... + а_nх_n делится на с.

10°. Если ас делится на вс, причем с ≠ 0, то а делится на в, т.е. (ас вс Ù с ≠ 0) Þ а в.

Доказательство.

ас = вс · к; ас = (вк) · с Ù с ≠ 0 Þ а = вк => а в.

Не нашли, что искали? Воспользуйтесь поиском: