Основная теорема арифметики

Важнейшим вопросом, связанным с простыми числами, является вопрос о возможности разложения любого числа на простые множители.

Условились считать два разложения на множители одинаковыми, если они отличаются друг от друга лишь порядком множителей. Например, одинаковы разложения 2 · 2 · 3 · 5 и 3 · 2 · 5 · 2. Тогда справедлива следующая теорема, которую называют основной теоремой арифметики натуральных чисел.

Теорема. Всякое натуральное число, большее единицы, можно единственным образом представить в виде произведения простых множителей.

Основной эта теорема называется потому, что практически все свойства делимости чисел являются ее следствиями.

Теорема содержит два утверждения:

1) разложение на простые множители существует,

2) разложение на простые множители единственно.

Предварительно сделаем замечание. Возникает вопрос: в каком смысле сформулированная теорема верна для простого числа р?

Условимся считать, что простое число представимо в виде произведения так: р = р, т.е. число простых множителей в правой части равно одному.

1) Докажем сначала возможность представления натурального числа большего единицы в виде произведения простых чисел.

Пусть п > 1– какое-нибудь натуральное число. Оно имеет по крайней мере один простой делитель р ₁, п = р ₁· п ₁, при этом п ₁ = 1 или п ₁ > 1. Если п ₁ = 1, то п = р ₁ и теорема доказана. Если число п ₁ > 1, то оно имеет хотя бы один простой делитель р ₂, т.е. n ₁ = p ₂ × n ₂,
n = p ₁ · p ₂ · n ₂. При этом п ₂ = 1 или п ₂ > 1. Если п ₂ = 1, то n ₁ = р ₂ и
n=p ₁ × p ₂ и теорема доказана. Если п ₂ > 1, то п ₂ имеет по крайней мере один простой делитель р ₃, п ₂ = p_{3 ×} n₃, п = p ₁ × p ₂ × p ₃ × n ₃, если п ₃ = 1, то
n = p ₁· p ₂· p ₃ и теорема доказана. Если п ₃ > 1, то рассуждаем аналогичным образом дальше.

Заметим, что числа n ₁, n ₂, n ₃, … уменьшаются: n ₁ > n ₂ > n ₃ > …. Но множество натуральных чисел, меньших определённого числа n, конечно. Поэтому проводимый нами процесс после конечного числа шагов должен прекратиться, что может наступить лишь при условии, что какое-либо число n_к = 1. Но тогда n = p ₁ · p ₂· … · p_к, где p ₁, p ₂, …, p_к – простые числа.

Этим и доказывается возможность представления любого натурального числа большего 1 в виде произведения простых чисел.

Процесс разложения натурального числа на простые множители, применённый при доказательстве, хорошо известен со школы и схематически изображается так

Для осуществления этого разложения испытывают, последовательно, делится ли n на простые числа 2, 3, 5, 7.

2) Доказательство единственности (от противного).

Допустим, что натуральное число n > 1 можно представить в виде произведения простых чисел не единственным образом:

n = p ₁· p ₂· … · p_к и n = q ₁ · q ₂ · … · q_m, где простые числа p_i могут отличаться от q_i, и, может быть, к ≠ m.

По симметричности и транзитивности отношения равенства имеем p ₁· p ₂ · … · p_к = q ₁· q ₂ · … · q_m (*). Правая часть имеет множителем q ₁, значит произведение в левой части делится на q ₁, но тогда по теореме 5 (§ 9) один из множителей делится на q ₁. Меняя в случае надобности места множителей, можем считать, что p ₁ q _{1 ,} но p ₁и q ₁ – простые числа, значит по теореме 6 (§ 9) p ₁ = q ₁. Разделим обе части равенства (*) на р ₁, получим:

p ₂ · p ₃ · … · p_к = q ₂ · q ₃ · … · q_m.

Аналогично устанавливаем, что один из множителей q ₂, q ₃, …, q_m равен р ₂. Пусть q ₂ = р ₂, тогда p ₃ · p ₄ · … · p_к = q ₃ · q ₄ · … · q_m. Повторяя рассуждения, придем:

1) при к = т к тому, что при сокращении всех множителей в левой части равенства (*) сократятся все множители в правой части равенства (*) и в этом случае два представления числа n, указанные при допущении, могут отличаться только порядком следования множителей;

2) при к < т к невозможному равенству 1 = q_{k +1} · q_{k +2} · … · q_m, т.к. произведение простых чисел не может быть равно единице;

3)при к > т придем к невозможному равенству

p_{m +1} · p_{m +2} · … · p_k = 1.

Следовательно, утверждение о единственности представления натурального числа п > 1 в виде произведения простых чисел доказано.

Если среди множителей p ₁, p ₂, …, p_к встречаются одинаковые, то, пользуясь записью произведения равных множителей как степени, можем написать: , где каждый из показателей – натуральное число, а все множители p ₁, p ₂, …, p_к – различные простые числа.

Такое представление натурального числа п > 1 называют каноническим разложением числа n на простые множители. Например,
360 = 2³ · 3² · 5.

14. Нахождение наибольшего общего делителя
и наименьшего общего кратного
способом разложения на простые множители

Если натуральные числа а и в представлены в каноническом виде, то над ними легко выполнять умножение, деление, возведение в степень.

Пусть ,

.

.

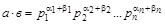, для a_к ≥ b _к,при к = 1, 2, …, n.

Из последнего равенства следует, что число d может быть общим делителем чисел а и в лишь в том случае, когда показатель степени каждого простого числа в разложении d не превосходит соответствующих показателей в числах а и в.

Иными словами при условии, что для любого к
(1 ≤ к ≤ n) будут выполняться неравенства g_к ≤ a_к и g_к ≤ b _к. НОД (а, в) – это наибольшее из чисел на которое делятся числа а и в. Значит, для каждого из простых чисел показатель степени в разложении НОД (а, в) должен быть наибольшим из возможных (т.е. удовлетворяющих неравенствам g_к ≤ a_к и g_к ≤ b _к). Этим показателем является меньшее из чисел a_к и b _к. Таким образом, чтобы найти НОД чисел, представленных в каноническом виде, достаточно образовать произведение общих всем данным числам простых множителей, каждый с наименьшим показателем, с каким он входит во все разложения данных чисел, и найти его значение.

Аналогично выводится и правило нахождения НОК: чтобы найти НОК чисел, представленных в каноническом виде, достаточно образовать произведение всех простых множителей, находящихся в разложениях данных чисел, каждый с наибольшим показателем, с каким он входит во все разложения данных чисел, и найти его значение.

П р и м е р. Найти НОК и НОД чисел 504 и 132

504 = 2³ ·3² · 7; 132 = 2² · 3 ·11.

НОД (504, 132) = 2² · 3 · 7⁰ · 11⁰ =12,

НОК (504, 132) = 2³ · 3² · 7 · 11 = 5544.

15. Некоторые свойства наибольшего общего делителя (НОД)
и наименьшего общего кратного (НОК)

Теорема 1 (О связи НОД и НОК). НОД (а, в) · НОК (а, в) = а · в.

Доказательство. Пусть и , тогда , используя ассоциативность и коммутативность умножения, перегруппируем множители следующим образом:

а × в = ,

где d_i ≤ t_i, i = 1, 2, …, к.

Т.е. поступили мы так: выбрали и и сравнили a_i и b _i. Если a _i ≥ b _i, то во 2-ой скобке, а – в 1-ой скобке. Но ведь тогда

,

,

т.е. а · в =НОД(а, в)·НОК(а, в).

П р и м е р.

Запишем равенство 12 ·240 = 60 · 48, получим 2880 = 2880.

Теорема 2 (облегчающая вычисление НОД и НОК).

1) НОД (а ₁, а ₂, … а _n) =НОД (НОД(а ₁, а ₂), а ₃, …, а_n),

2) НОК (а ₁, а ₂, … а _n) =НОК (НОК(а ₁, а ₂), а ₃, …, а_n).

Теорема позволяет при отыскании НОД и НОК нескольких чисел производить это последовательно, заменяя пару чисел их НОД и НОК.

Доказательство. 1) Пусть даны числа а ₁, а ₂, …, а_n своими каноническими разложениями.

,

,

,

… …….. …….

.

НОД (а ₁, а ₂) = , где t_i – наименьшее из чисел a_i, b_i, i = 1, 2, …, к.

Обозначим через d_i – наименьшее из чисел a_i, b_i, c_i, …, g_i, тогда d_i является наименьшим из чисел t_i, c_i, …, g_i.

НОД , отсюда

НОД(а ₁, а ₂, …, а_n) = НОД (НОД (а ₁, а ₂), а ₃, а ₄, …, а_n).

2) Точно так же доказывается и вторая часть.

НОК , где r _i – наибольшее из чисел a_i, b_i, i = 1, 2, …, к.

НОК , где m_i – наибольшее из чисел a_i, b_i, c_i, …, g_i и является наибольшим из чисел r_i, c_i, …, g_i, отсюда

НОК (а ₁, а ₂, …, а_n) = НОК (НОК (а ₁, а ₂), а ₃, а ₄, …, а_n).

П р и м е р. Применяя теорему 2, найдем НОД (1320, 3600, 1485).

1320 = 2³ · 3¹ · 5 · 11,

3600 = 2⁴ · 3² · 5² ·11⁰,

1485 = 2⁰ · 3³ · 5 · 11.

НОД (1320, 3600) = 2³ · 3 · 5 = 120,

НОД (120, 1485) = 2⁰ · 3 · 5 = 15.

Значит, НОД (1320, 3600, 1485) = 15.

НОК (1320, 3600) = 2⁴ · 3² · 5² · 11 = 39600

НОК (39600, 1485) = 2⁴ · 3³ · 5² · 11 = 118800.

Значит, НОК (1320, 3600, 1485) = 118800.

Теорема 3. Пусть m – некоторое натуральное число, тогда

НОД (ma₁, ma₂, …, ma_n) = m НОД (а ₁, а ₂, …, а_n),

НОК (ma₁, ma₂, …, ma_n) = m НОК (а ₁, а ₂, …, а_n), то есть общий множитель можно выносить за знак НОД и за знак НОК.

Доказательство. Запишем каноническое разложение чисел 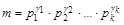, НОД (а ₁, а ₂, …, а_n) = ,

НОК (а ₁, а ₂, …, а_n) = . Ясно, что есть наименьший, а – наибольший среди степеней простого числа p_i, встречающихся в канонических разложениях чисел а ₁, а ₂, …, а_n, но тогда 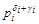будет наименьшим, а – наибольшим среди степеней простого числа p _i в разложениях чисел mа ₁, mа ₂, …, mа_n. p_i – это любое число из простых множителей чисел а ₁, а ₂, …, а_n. Значит, получили m НОД (а ₁, а ₂, …, а_n) = = НОД (mа ₁, mа ₂, …, mа_n).

Аналогично, m НОК (а ₁, а ₂, …, а_n) = = НОК (mа ₁, mа ₂, …, mа_n).

Следствие 1.

Пусть m – есть некоторый общий делитель чисел в ₁, в ₂, …, в_n, тогда

НОД ;

НОК ,

т.е. если данные числа разделить на m, то их НОД и НОК также разделятся на m.

Доказательство. По теореме 3 имеем:

m НОД (а ₁, а ₂, …, а_n) = НОД (mа ₁, mа ₂, …, mа_n), разделим обе части равенства на m, получим

НОД (а ₁, а ₂, …, а_n) = .

Обозначим ma_i = в_i Þ a_i = . Тогда:

. Что и требовалось доказать. Точно также выводится равенство относительно НОК.

Следствие 2.

d = НОД (а ₁, а ₂, …, а_n)Û .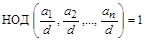

Доказательство. Необходимость.

Дано НОД (а ₁, а ₂, …, а_n) = d, доказать, что .

По следствию 1, имеем

НОД .

Достаточность.

Дано НОД , доказать, что НОД (а ₁, а ₂, …, а_n) = d.

Обе части данного равенства умножим на d,

тогда d НОД .

По теореме 2 НОД (а ₁, а ₂, …, а_n) = d. Что и требовалось доказать.

П р и м е р ы на применение следствия.

Пусть в₁ = 33, в₂ = 55, в₃ = 99 Þ m = 11

1. .

=НОК (3, 5, 9) Þ НОК (33, 55, 99) = 11 · 45 = 495.

2. Пусть в ₁ = 33, в ₂ = 55, в ₃ = 99;

НОД (33, 55, 99) = 11. Тогда НОД ()= 1.

Не нашли, что искали? Воспользуйтесь поиском: