Признаки делимости на 4 и 25.

Число тогда и только тогда делится на 4, когда две его последние цифры образуют число, делящееся на 4.

Число тогда и только тогда делится на 25, когда две его последние цифры образуют число, делящееся на 25, т.е. 00, 25, 50, 75.

Доказательство. Заметим, что числа 4 и 25 делители числа 100. Пусть S любое натуральное число, в десятичной системе счисления его можно представить так:

S = а_п · 10 ⁿ + а_{n- 1} · 10 ^{n -1} +... + а ₂ × 10² + а ₁ · 10 + а ₀.

Все слагаемые, кроме последних двух, содержат множителем число 100, а потому они делятся на 4 и 25.

Делится ли S на 4 и на 25 зависит от суммы слагаемых а ₁ · 10 + а ₀,т.е. от числа, образованного последними двумя цифрами. Для того, чтобы S делилось на 4, достаточно чтобы а ₁ · 10+ а ₀делилось на 4. Обратное утверждение тоже верно.

Для того, чтобы S делилось на 25, достаточно чтобы а ₁ · 10 + а ₀делилось на 25, т.е. чтобы S оканчивалось на 00, 25, 50, 75. Обратное утверждение тоже верно.

Значит, S 4 Û (а ₁ · 10 + а ₀) 4; S 25 Û (а ₁ · 10 + а ₀) 25.

. 5. Признаки делимости в других позиционных
системах счисления

Приведем некоторые признаки делимости в других, отличных от десятичной, позиционных системах счисления.

Пусть основание системы счисления равно р.

Если р а, то все числа вида р ², р ³,..., рⁿ делятся на а, тогда и сумма а_nрⁿ + а_{n -1} р^{n -1} +... + а₁р делится на а. Поэтому, если р делится на а и число х имеет в системе счисления с основанием р запись

х = а_nрⁿ +... + а ₁ р + а₀,то х a Û а ₀ a.

Например, в двенадцатиричной системе счисления число делится на 3 тогда и только тогда, когда его последняя цифра равна 0, 3, 6 или 9. Признак вытекает из того, что 12 3. Точно также

х ₁₂ 4 Û а ₀ 4, х ₁₂ 6 Û а ₀ 6.

Пусть снова р есть основание системы счисления. Приведем признак делимости числа х на (р – 1).Предварительно заметим, что

pⁿ – 1 = (p – 1)(p^{n- 1} + p^{n- 2} + … + 1).

В частности, p ² – 1 = (p – 1)(p + 1),

p ³ – 1 = (p – 1)(p² + p + 1),

p ⁴ – 1 = (p – 1)(p ³ + p ² + p + 1).

Запишем число x таким образом:

.

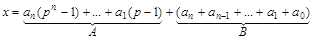Первая сумма A делится на число p – 1 и его делители (по сделанному выше замечанию), потому делимость числа x зависит от суммы B.

.

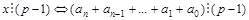Например, в двенадцатеричной системе счисления число делится на 11 тогда и только тогда, когда сумма его цифр делится на 11.

П р и м е р. Дано число 675120₈. Делится ли оно на 7? Для ответа на вопрос найдём сумму цифр 6 + 7 + 5 + 1 + 2 + 0 = 25₈. 25₈ : 7 = 3.

Значит, 675120₈ 7.

6. Четыре класса целых неотрицательных чисел.
Простые и составные числа

Число 0 имеет бесконечно много делителей. Число 1 имеет единственный делитель 1. Любое натуральное число а > 1 имеет конечное число делителей, а в Þ 1 ≤ в ≤ а, т.е. в может принимать не более чем а различных значений.

Определение. Натуральное число, большее 1, называется простым, если оно делится только на себя и на 1. Натуральное число а называется составным, если а d, где 1 < d < а.

По числу различных натуральных делителей множество целых неотрицательных чисел N ₀ разбивается на четыре попарно непересекающихся подмножества (класса):

1) число 1 (имеет один натуральный делитель);

2) числа простые (имеют точно два натуральных делителя);

3) числа составные (имеют не менее трех различных натуральных делителей);

4) число 0 (имеет бесконечно много натуральных делителей).

Теорема 1 (о существовании простого делителя).

Если натуральное число а > 1,то оно имеет хотя бы один простой делитель.

Доказательство (методом от противного).

Пусть дано число а. Обозначим буквой d –наименьший среди натуральных делителей числа а, больших единицы. Предположим, что d не является простым числом, а значит имеет делитель t.

Т.е. d t Ù t < d, докажем, что t = 1. Т.к. а d Ù d t Þ а t, но ведь это означает, что t еще меньший, чем d делитель числа а, что противоречит выбору d, значит t = 1,т.е. d имеет только два натуральных делителя d и 1.

Теорема 2. Наименьший простой делитель составного числа а не превосходит .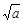

Доказательство. Пусть дано число а. Обозначим буквой р его наименьший простой делитель, тогда а = р · в, при этом р ≤ в, т.к. иначе простой делитель числа в был бы меньше, чем р. Тогда а имело бы простые делители меньшие, чем р. Умножим левую и правую часть неравенства р ≤ в на р, получим р ² ≤ р · в = а Þ р ≤ .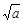

Следствие. Если число а не делится ни на одно простое число, не превосходящее 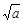, то у него нет совсем простых делителей, меньших этого числа, т.е. это число простое.

Например, 137 простое число. В самом деле, 1l < 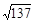< 12, если 137 не делится на простые числа меньшие 12, то оно простое. 137 не делится на 2, на 3, на 5, на 7, на 11. Вывод: 137 – простое число.

Не нашли, что искали? Воспользуйтесь поиском: