Контрольная работа №4. 171 – 180.Если закон движения точки на прямой задан функцией , то

171 – 180.Если закон движения точки на прямой задан функцией , то . Для нахождения нужно найти критические точки функции , вычислить значение в критических точках, принадлежащих отрезку 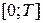, и на концах этого отрезка и выбрать из полученных значений наибольшее по модулю. Точно так же находим .

181 – 190.Функция называется первообразной для функции 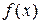, если . Совокупность всех первообразных для функции 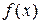называется неопределенным интегралом от функции 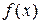и обозначается , при этом 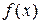называется подынтегральной функцией, 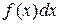– подынтегральным выражением.

Можно доказать, что 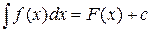, где – некоторая первообразная для 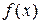, – произвольная постоянная.

Для вычисления неопределенных интегралов нужно знать основные свойства, табличные интегралы и методы интегрирования.

Основные свойства неопределенных интегралов:

1. .

2. , где – постоянная, не равная нулю.

3. .

4. .

Свойства 3 и 4 показывают, что операции дифференцирования и интегрирования являются взаимообратными.

Таблица неопределенных интегралов

1)

2)

3)

Если 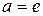, то .

4)

5)

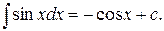
6)

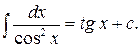
7)

8)

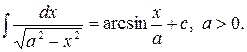
9)

10)

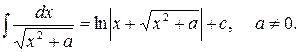
11)

Все формулы справедливы также в случае, если переменную заменить на некоторую другую функцию. Так, если в формуле 2 заменить на 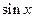, то получим,

.

Перейдем к рассмотрению методов интегрирования.

Не нашли, что искали? Воспользуйтесь поиском: