Интегрирование по частям (181-190, б)

Формула интегрирования по частям имеет вид

,

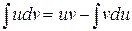поскольку 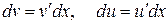, то эту же формулу можно записать так:

.

Для того чтобы применить формулу интегрирования по частям, нужно подынтегральную функцию разбить на два множителя, один из них обозначить , другой − 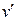. После этого найти 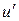и . Для нахождения функции по заданной производной 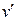можно вычислить неопределенный интеграл 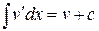и затем положить .

При выборе функций и 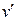следует помнить, что функция 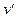не должна быть сложной, иначе для нее будет трудно найти первообразную. В качестве обычно выбирают функцию, которая упрощается при дифференцировании, например, логарифмическую или обратную тригонометрическую функцию. В частном случае за можно взять подынтегральную функцию, тогда и .

Пример. Вычислить .

Решение. Положим 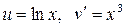. Тогда .

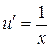Найдем ; .

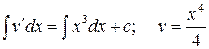Применим формулу интегрирования по частям:

.

Не нашли, что искали? Воспользуйтесь поиском: