
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Геометрические приложения определенного интеграла .
Пусть функция  непрерывна и неотрицательна на
непрерывна и неотрицательна на  . Тогда площадь
. Тогда площадь 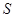 криволинейной трапеции
криволинейной трапеции 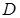 (рис.5), ограниченной графиком функции
(рис.5), ограниченной графиком функции  , осью
, осью  и прямыми
и прямыми  вычисляется по формуле
вычисляется по формуле
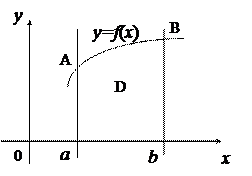
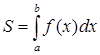 .
.
|
Рис. 5
Длина дуги 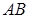 , заданной графиком функции
, заданной графиком функции  , вычисляется по формуле
, вычисляется по формуле
 .
.
Если функция  задана параметрически уравнениями
задана параметрически уравнениями  ,
,  , где
, где  , то
, то
 ,
, 
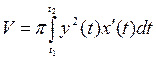 ,
,
 .
.
Пусть в полярной системе координат задана функция  , где
, где  – полярный угол,
– полярный угол,  – полярный радиус точки.
– полярный радиус точки.
| |||
 | |||
Рис. 6
Длина дуги вычисляется по формуле 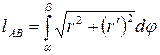 .
.
Пример. Вычислить длину одной арки циклоиды  ,
,  ,
, 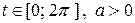 .
.
Решение. Нарисуем арку циклоиды (рис. 7). Заметим, что если 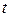 меняется от 0 до
меняется от 0 до  , то
, то  возрастает от 0 до
возрастает от 0 до  , а
, а  сначала возрастает от 0 до
сначала возрастает от 0 до 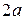 , а затем убывает до 0.
, а затем убывает до 0.
 | |||||||
 | |||||||
 | |||||||
 |
Рис. 7

 .
.
211 − 220. Несобственные интегралы – это обобщение понятия определенного интеграла для случая, когда либо неограниченным является промежуток интегрирования, либо неограничена подынтегральная функция на отрезке интегрирования. Рассмотрим эти два случая.
1. Пусть функция 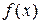 непрерывна на
непрерывна на  , тогда
, тогда  называется несобственным интегралом от функции
называется несобственным интегралом от функции 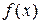 на промежутке
на промежутке  и обозначается
и обозначается 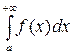 , т.е.
, т.е.
 ,
,
при этом, если существует конечный предел, говорят, что несобственный интеграл сходится, в противном случае – расходится.
Аналогично
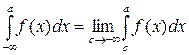 ,
,
 , (1)
, (1)
при этом несобственный интеграл в левой части формулы (1) называется сходящимся, если оба несобственных интеграла в правой части формулы (1) сходятся (число а в формуле (1) можно выбрать произвольно).
2. Пусть функция 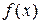 непрерывна на
непрерывна на  и
и  , тогда
, тогда  называется несобственным интегралом и обозначается
называется несобственным интегралом и обозначается  , т.е.
, т.е.
 ,
,
при этом, если существует конечный предел, то несобственный интеграл называется сходящимся.
Возможны другие случаи, например,
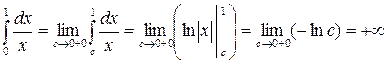 .
.
Следовательно, несобственный интеграл 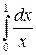 расходится.
расходится.
Не нашли, что искали? Воспользуйтесь поиском:
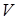 тела, образованного вращением криволинейной трапеции
тела, образованного вращением криволинейной трапеции  .
.
 непрерывна на
непрерывна на  , то площадь криволинейного сектора
, то площадь криволинейного сектора  , ограниченного графиком функции
, ограниченного графиком функции  ,
,  (рис. 6), вычисляется по формуле:
(рис. 6), вычисляется по формуле:
 .
.