Интегрирование рациональных функций (181-190, г)

Отношение двух многочленов называется рациональной функцией. Если степень многочлена в числителе меньше степени многочлена в знаменателе, то рациональная функция называется правильной, в противном случае – неправильной. Простейшими рациональными функциями называются функции вида

,

где – действительные числа; – натуральное число и .

Алгоритм интегрирования рациональной функции:

1. Если рациональная функция неправильная, то с помощью деления ее нужно представить в виде суммы многочлена и правильной рациональной функции.

2. Знаменатель правильной рациональной функции нужно разложить на линейные и квадратичные множители.

3. Используя метод неопределенных коэффициентов, разложить правильную рациональную функцию на сумму простейших.

4. Проинтегрировать все полученные слагаемые.

Пример. Вычислить .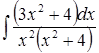

Подынтегральная функция правильная, и ее знаменатель разложен на множители, поэтому переходим к третьему пункту алгоритма. Разложение на сумму простейших для этой функции будет иметь вид

,

где – некоторые числа (неопределенные коэффициенты), которые нужно найти. Дроби в правой части приводим к общему знаменателю (он равен ) и приравниваем числители.

.

Приравнивая коэффициенты при одинаковых степенях в левой и правой части, получим систему уравнений.

Таким образом,

.

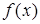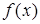1912200.Если – непрерывная функция на и – первообразная для , то определенный интеграл можно вычислить по формуле Ньютона-Лейбница

.

Пример.

.

При вычислении определенного интеграла можно использовать формулу интегрирования по частям:

.

(функции и должны быть непрерывны на ).

Пример.

.

В определенном интеграле можно сделать замену переменной , тогда

,

где числа 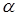и такие, что 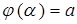, (функция 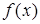должна быть непрерывна на , функция – непрерывна на ).

201 − 210.

Не нашли, что искали? Воспользуйтесь поиском: