
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Примеры решения задач. Пример 1.Материальная точка движется по плоскости согласно уравнению , где ;
Пример 1. Материальная точка движется по плоскости согласно уравнению 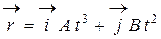 , где
, где 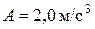 ;
; 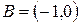
 . Для момента времени
. Для момента времени  вычислить: 1) модуль скорости
вычислить: 1) модуль скорости 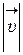 ; 2) модуль ускорения
; 2) модуль ускорения  ;
;
3) модуль касательного ускорения 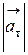 ; 4) модуль нормального ускорения
; 4) модуль нормального ускорения 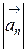 .
.
Дано:  , где
, где 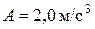 ;
; 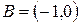
 .
.  .
.
Найти: 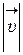 ,
, 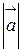 ,
,  ,
, 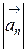 .
.
Решение: Выпишем формулу для радиус-вектора плоского движения материальной точки:
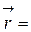
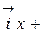
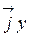 .
.
Сравнивая ее с данной в задаче зависимостью
 ,
,
получим, что векторному уравнению соответствуют два уравнения для зависимости координат от времени:
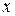 =
= 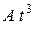 ; y =
; y =  . (1)
. (1)
Модуль вектора скорости определяется через его проекции по общему для всех векторов правилу:
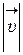 =
=  . (2)
. (2)
где 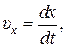
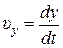 – проекции скорости на координатные оси
– проекции скорости на координатные оси  .
.
Выполнив дифференцирование выражений (1), находим обе проекции скорости:

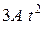 ,
, 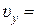
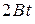 . (3)
. (3)
Выражение модуля вектора мгновенной скорости (2) примет вид:
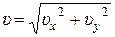 =
= 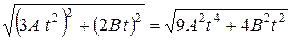 . (4)
. (4)
Выполним вычисление мгновенной скорости в заданный момент времени  :
:
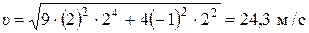 .
.
Теперь воспользуемся формулой модуля вектора полного ускорения через его проекции на координатные оси
 ,
,
где 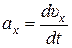 ;
;  .
.
Выполнив дифференцирование выражений (3), находим обе проекции ускорения:
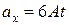 ;
; 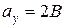 .
.
Выражение модуля мгновенного ускорения примет вид:
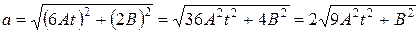 .
.
Выполним вычисления модуля мгновенного ускорения в заданный момент времени  :
:
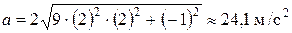 .
.
Модуль касательного ускорения 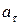 есть первая производная модуля скорости по времени, выполним дифференцирование выражения модуля мгновенной скорости (4), получим выражение
есть первая производная модуля скорости по времени, выполним дифференцирование выражения модуля мгновенной скорости (4), получим выражение 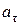 :
:
 .
.
Выполним вычисления модуля касательного ускорения в момент времени  :
:
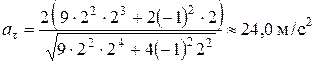 .
.
Полное ускорение, как это видно из рис. 1, является геометрической суммой ускорений 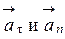 :
: 
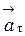 +
+ 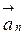 .
.
Модули ускорений связаны соотношением
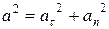 .
.
Откуда
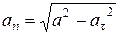 .
.
Выполним вычисления нормального ускорения в заданный момент времени  :
:
 .
.
Ответ: 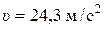 ;
; 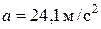 ;
; 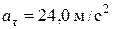 ;
; 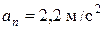 .
.
Пример 2. Тело брошено со скоростью  под углом
под углом 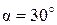 к горизонту. Пренебрегая сопротивлением воздуха, найти расстояние l, на которое переместится тело по горизонтали, и на какой высоте h окажется в момент времени
к горизонту. Пренебрегая сопротивлением воздуха, найти расстояние l, на которое переместится тело по горизонтали, и на какой высоте h окажется в момент времени  после начала движения.
после начала движения.
Дано:  ;
; 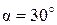 ;
;  .
.
Найти: l, h.
Решение: Так как тело движется с постоянным ускорением 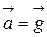 , его скорость и перемещение определяется векторными уравнениями
, его скорость и перемещение определяется векторными уравнениями
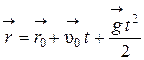 ,
,

и соответствующими им скалярными уравнениями
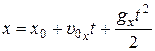 ;
; 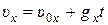 ; (1)
; (1)
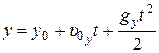 ;
; 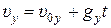 . (2)
. (2)
Введем координатные оси, направленные по горизонтали  и вертикали
и вертикали  и совместим начало координат с положением тела в начальный момент времени. Запишем координаты, проекции скорости и ускорения на координатные оси в начальный момент времени, рис. 6:
и совместим начало координат с положением тела в начальный момент времени. Запишем координаты, проекции скорости и ускорения на координатные оси в начальный момент времени, рис. 6:
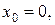
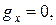
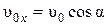 ,
,
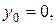
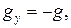
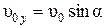 .
.
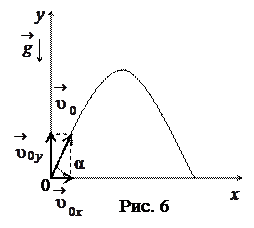 Подставив в уравнения (1), (2) начальные условия, получим
Подставив в уравнения (1), (2) начальные условия, получим
 , (3)
, (3)
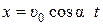 , (4)
, (4)
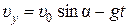 , (5)
, (5)
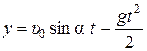 . (6)
. (6)
Искомые величины l, h равны соответственно координатам 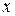 ,
, 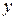 в момент времени
в момент времени  .
.

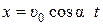 =
= 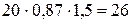 м.
м.

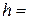
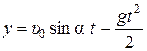 =
= 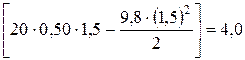 м.
м.
Ответ:  26 м;
26 м; 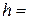 4,0 м.
4,0 м.
Пример 3. Маховик вращается равноускоренно. Найти угол  , который составляет вектор полного ускорения
, который составляет вектор полного ускорения 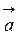 любой точки маховика с радиус-вектором
любой точки маховика с радиус-вектором  , проведенным по радиусу кривизны траектории (рис. 7) в тот момент, когда маховик совершит первые
, проведенным по радиусу кривизны траектории (рис. 7) в тот момент, когда маховик совершит первые 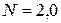 оборота.
оборота.
Дано: 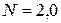 .
.
Найти: 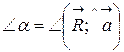 .
.
Решение: Выберем на маховике точку М, которая будет вращаться по окружности радиуса R (рис. 5). Разложим вектор полного ускорения 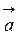 точки М на касательное
точки М на касательное 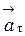 и нормальное
и нормальное 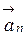 ускорения. Видим, что искомый угол
ускорения. Видим, что искомый угол  определяется соотношением
определяется соотношением
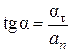 .
.
Поскольку в условии дано лишь число оборотов, перейдем к угловым величинам, применив формулы связи линейных параметров с угловыми:
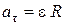 ;
; 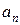 =
= 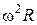 .
.
Тогда получим

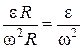 (1)
(1)
Так как маховик вращается равноускоренно, найдем связь между величинами 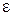 и
и  с помощью формул равнопеременного вращения:
с помощью формул равнопеременного вращения:
 ,
,
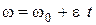 .
.
Исключив из последних уравнений время, получим

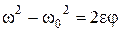 .
.
Поскольку 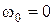 , а
, а 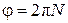 , то
, то

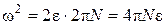 . (2)
. (2)
Подставив значение 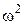 из (2) в (1), получим
из (2) в (1), получим
tg 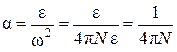 . (3)
. (3)
Выполним вычисления:
tg 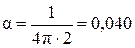 .
.
α = arctg 
Угол  , образуемый вектором
, образуемый вектором 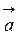 с радиус-вектором
с радиус-вектором  , одинаков для всех точек и целиком определяется углом поворота
, одинаков для всех точек и целиком определяется углом поворота 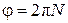 .
.
Ответ: 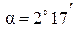 .
.
Пример 4 Тело массой m, находящееся на вершине наклонной плоскости, удерживается силой трения. За какое время тело спустится с наклонной плоскости, если плоскость станет двигаться в горизонтальном направлении с ускорением  (рис. 8)? Длина наклонной плоскости
(рис. 8)? Длина наклонной плоскости 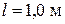 , угол наклона к горизонту
, угол наклона к горизонту 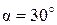 , коэффициент трения между телом и плоскостью
, коэффициент трения между телом и плоскостью 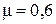 .
.
Дано:  ,
, 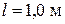 ,
, 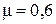 .
.
Найти: t.
Решение: Выберем систему отсчета, связанную с наклонной плоскостью. Пока плоскость покоится, на тело действуют три силы: сила тяжести 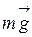 , сила нормального давления
, сила нормального давления 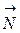 опоры и сила трения покоя
опоры и сила трения покоя 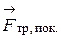 , которые уравновешивают друг друга.
, которые уравновешивают друг друга.
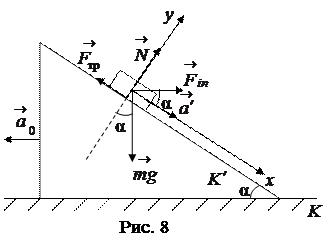 Как только начнется ускоренное движение плоскости и «привязанная», к ней система отсчета
Как только начнется ускоренное движение плоскости и «привязанная», к ней система отсчета 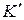 станет неинерциальной, появится четвертая сила – сила инерции
станет неинерциальной, появится четвертая сила – сила инерции 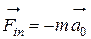 (рис. 6). Равновесие нарушится, тело начнет скользить вниз по наклонной плоскости с ускорением
(рис. 6). Равновесие нарушится, тело начнет скользить вниз по наклонной плоскости с ускорением 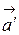 . Для решения задачи применяем уравнение движения тела в неинерциальной системе отсчета
. Для решения задачи применяем уравнение движения тела в неинерциальной системе отсчета
 , (1)
, (1)
где 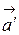 – ускорение тела в неинерциальной системе отсчета;
– ускорение тела в неинерциальной системе отсчета;
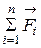 – векторная сумма сил, обусловленных воздействием тел друг на друга, (
– векторная сумма сил, обусловленных воздействием тел друг на друга, (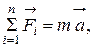
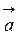 – ускорение в инерциальной системе),
– ускорение в инерциальной системе), 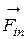 – сила инерции.
– сила инерции.
Согласно условиям задачи уравнение (1) перепишем в виде:
 . (2)
. (2)
Выберем оси проекций, как показано на рис. 8. Проектируя все вектора, входящие в уравнение (2) на оси 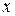 и
и 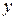 , получим соответственно два скалярных уравнения:
, получим соответственно два скалярных уравнения:
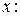
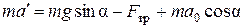 . (3)
. (3)
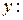
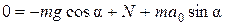 . (4)
. (4)
Решаем систему уравнений (3), (4) с учетом того, что сила трения скольжения 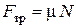 , и находим выражение для ускорения
, и находим выражение для ускорения  :
:
 . (5)
. (5)
Искомое время движения тела по плоскости определяем из известной формулы пути равноускоренного движения без начальной скорости  :
:
 (6)
(6)
Подставив в формулу (6) выражение (5) для ускорения  , получаем
, получаем
 .
.
Выполняем вычисления:
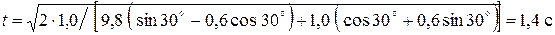 .
.
Ответ: 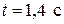 .
.
Пример: 5. На железнодорожной платформе массой 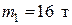 установлено орудие массой
установлено орудие массой 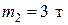 , ствол которого расположен под углом
, ствол которого расположен под углом  к горизонту (рис. 9). Чему равна скорость снаряда массой
к горизонту (рис. 9). Чему равна скорость снаряда массой 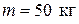 , если после выстрела платформа приобрела скорость
, если после выстрела платформа приобрела скорость 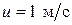 .
.
Дано: 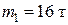 ,
, 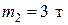 ,
, 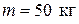 ,
,  ,
, 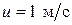 .
.
Найти: 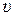 – скорость снаряда.
– скорость снаряда.
Решение. Система состоит из платформы, орудия и снаряда. Начальное состояние системы соответствует неподвижной платформе, орудию и снаряду. Конечное состояние – сразу после выстрела. Импульс системы не сохраняется, так как во время выстрела действует внешняя некомпенсированная сила со стороны Земли – сила тяжести, которая направлена вертикально. Следовательно, во время выстрела система не является замкнутой, ее импульс изменяется. Однако внешние силы действуют по вертикали, в то время как в горизонтальном направлении никакие силы не действуют (трением платформы о рельсы пренебрегаем).
 Поэтому проекция импульса системы на горизонтальное направление (ось
Поэтому проекция импульса системы на горизонтальное направление (ось 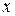 , рис. 9) есть величина постоянная:
, рис. 9) есть величина постоянная:
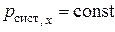 (1)
(1)
Пусть состоянием системы до и после выстрела соответствуют значения величины 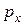 , равные
, равные 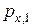 и
и 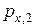 . С учетом введенных обозначений перепишем уравнение (1):
. С учетом введенных обозначений перепишем уравнение (1):
 ,
,
или  ,
,
где 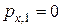 – проекция импульса системы до выстрела,
– проекция импульса системы до выстрела, 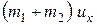 – проекция импульса платформы с орудием после выстрела,
– проекция импульса платформы с орудием после выстрела, 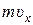 – проекция импульса снаряда после выстрела.
– проекция импульса снаряда после выстрела.
Так как 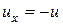 и
и 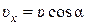 ,
,

 .
.
Откуда  .
.
Выполним вычисления:
 .
.
Ответ: 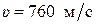 .
.
Пример: 6. Тонкий однородный стержень длины 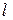 может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов (рис. 10). Стержень приводят в горизонтальное положение и отпускают. Определить угловое ускорение и угловую скорость стержня при прохождении стержнем положения равновесия.
может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов (рис. 10). Стержень приводят в горизонтальное положение и отпускают. Определить угловое ускорение и угловую скорость стержня при прохождении стержнем положения равновесия.
Дано: 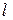 .
.
Найти: 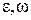 .
.
Решение. Стержень поворачивается вокруг оси под действием момента силы тяжести. Так как при опускании стержня этот момент уменьшается за счет уменьшения плеча силы 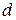 , то вращение стержня не будет равнопеременным. Поэтому для нахождения углового ускорения рассмотрим стержень в некоторый момент его движения (положение II).
, то вращение стержня не будет равнопеременным. Поэтому для нахождения углового ускорения рассмотрим стержень в некоторый момент его движения (положение II).
 Воспользуемся основным законом динамики вращательного движения твердого тела относительно оси вращения z.
Воспользуемся основным законом динамики вращательного движения твердого тела относительно оси вращения z.
 , (1)
, (1)
где 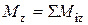 – результирующий момент всех внешних сил, приложенных к телу,
– результирующий момент всех внешних сил, приложенных к телу, 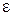 – его угловое ускорение,
– его угловое ускорение,  – момент инерции стержня относительно одной и той же оси z.
– момент инерции стержня относительно одной и той же оси z.
На стержень действуют сила тяжести 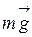 , приложенная в центре масс, и сила реакции оси
, приложенная в центре масс, и сила реакции оси 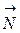 . Вращающий момент создает только сила тяжести, т.к. линия действия силы реакции оси
. Вращающий момент создает только сила тяжести, т.к. линия действия силы реакции оси 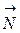 проходит через ось вращения. Уравнение (1) перепишем, учитывая, что момент силы тяжести относительно оси равен произведению силы тяжести
проходит через ось вращения. Уравнение (1) перепишем, учитывая, что момент силы тяжести относительно оси равен произведению силы тяжести  на плечо этой силы:
на плечо этой силы:
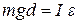 , (2)
, (2)
где 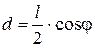 – плечо силы тяжести.
– плечо силы тяжести.
Момент инерции стержня относительно оси z, проходящей через один конец, равен
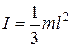 . (3)
. (3)
Подставив в уравнение (2) выражение момента инерции (3) и плеча силы тяжести d, получим
 ,
,
откуда
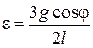 . (4)
. (4)
Как видно из формулы (4), угловое ускорение зависит от угла 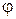 и в процессе движения стержня из горизонтального положения до положения равновесия убывает, не изменяя своего направления. В положении равновесия
и в процессе движения стержня из горизонтального положения до положения равновесия убывает, не изменяя своего направления. В положении равновесия  , угловое ускорение
, угловое ускорение
 .
.
Для нахождения угловой скорости 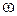 воспользуемся законом сохранения механической энергии, так как движение стержня происходит под действием силы тяжести, а сила реакции оси работы не совершает. При переходе из положения I в положение равновесия III.
воспользуемся законом сохранения механической энергии, так как движение стержня происходит под действием силы тяжести, а сила реакции оси работы не совершает. При переходе из положения I в положение равновесия III.
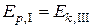 ,
,
где  – есть потенциальная энергия поднятого стержня, если принять нулевой уровень отсчета высоты (
– есть потенциальная энергия поднятого стержня, если принять нулевой уровень отсчета высоты (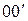 , рис. 10) проходящим через центр тяжести стержня в его нижнем положении,
, рис. 10) проходящим через центр тяжести стержня в его нижнем положении, 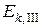 – кинетическая энергия вращательного движения стержня в нижнем положении.
– кинетическая энергия вращательного движения стержня в нижнем положении.
Следовательно,
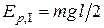 ,
,  ,
,
учитываем, что центр тяжести стержня был поднят в положение I на высоту 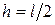 .
.
Приравниваем правые части последних двух равенств и учитывая, что момент инерции стержня 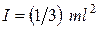 ,
, 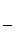 получаем
получаем

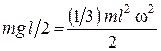 ,
,
откуда
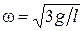 .
.
Ответ: 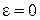 ,
, 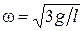 .
.
Пример 7. На горизонтальную ось насажен шкив радиуса R. На шкив намотан шнур, к свободному концу которого подвесили гирю массой 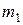 (рис. 11). Считая массу
(рис. 11). Считая массу 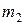 шкива равномерно распределенной по ободу, определить ускорение а, с которым будет опускаться гиря, силу натяжения Т нити.
шкива равномерно распределенной по ободу, определить ускорение а, с которым будет опускаться гиря, силу натяжения Т нити.
 Дано:
Дано: 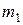 – масса гири;
– масса гири; 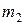 – масса шкива;
– масса шкива;
R – радиус шкива.
Найти: а – ускорение гири; Т – натяжение нити.
Решение. Поскольку ускорение центра инерции шкива  и шкив только вращается, то применяем основное уравнение динамики вращательного движения
и шкив только вращается, то применяем основное уравнение динамики вращательного движения
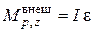 . (1)
. (1)
На шкив действуют силы тяжести 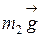 , натяжения нити
, натяжения нити 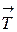 и реакция оси
и реакция оси 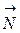 . Шкив вращается под действием лишь момента силы Т. Моменты сил тяжести
. Шкив вращается под действием лишь момента силы Т. Моменты сил тяжести 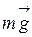 и реакции оси
и реакции оси 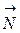 равны нулю, так как, линии действия этих сил проходят через ось вращения. Модуль момента силы
равны нулю, так как, линии действия этих сил проходят через ось вращения. Модуль момента силы 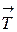 относительно оси
относительно оси
 ,
,
где R – плечо силы Т.
Момент инерции шкива, поскольку его масса распределена по ободу равномерно, найдем по формуле:
 .
.
Следовательно, уравнение (1) примет вид:
 . (2)
. (2)
Уравнение (2), описывающее движение шкива, содержит две неизвестных Т и 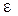 .
.
Недостающие величины найдем, рассмотрев движение груза. Применим второй закон Ньютона для поступательного движения груза:
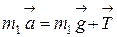 . (3)
. (3)
В проекциях на ось 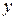 уравнение (3) примет вид
уравнение (3) примет вид
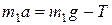 ,
,
откуда
 (4)
(4)
Поскольку шнур сматывается со шкива без проскальзывания, ускорение гири равно касательному ускорению 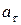 точек на ободе шкива.
точек на ободе шкива.
Следовательно,
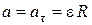 ;
; 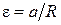 (5)
(5)
Подставив в (2) значения Т, 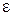 по формулам (4) и (5), получим неизвестные а и Т:
по формулам (4) и (5), получим неизвестные а и Т:
 ;
; 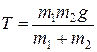 .
.
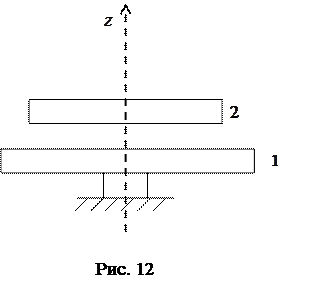
Пример 8. Диск 1 (рис. 12) вращается вокруг гладкой вертикальной оси с угловой скоростью  . На него падает диск 2, вращающийся с угловой скоростью
. На него падает диск 2, вращающийся с угловой скоростью 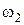 . Вследствие трения между ними оба диска через некоторое время начинают вращаться как единое целое. Найти приращение кинетической энергии вращения этой системы, если моменты инерции дисков относительно оси вращения равны соответственно
. Вследствие трения между ними оба диска через некоторое время начинают вращаться как единое целое. Найти приращение кинетической энергии вращения этой системы, если моменты инерции дисков относительно оси вращения равны соответственно 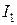 и
и 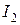 .
.
Дано:  – угловая скорость вращения диска 1;
– угловая скорость вращения диска 1; 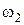 – угловая скорость вращения диска 2;
– угловая скорость вращения диска 2; 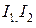 – момент инерции дисков относительно оси вращения z.
– момент инерции дисков относительно оси вращения z.
Найти: 
Решение. Сначала найдем установившуюся угловую скорость вращения дисков. Учтем, что, согласно условию задачи, диски вращаются по инерции. Это означает, что результатирующий момент всех внешних сил, приложенных к вращающимся дискам, равен нулю. Следовательно, для системы из дисков выполняется закон сохранения момента импульса
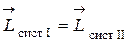
или в проекциях на ось вращения z:
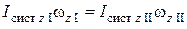 , (1)
, (1)
где 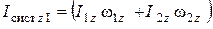 – момент импульса системы дисков относительно оси z до перемещения дисков;
– момент импульса системы дисков относительно оси z до перемещения дисков;
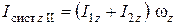 – момент импульса системы дисков относительно оси z после перемещения дисков.
– момент импульса системы дисков относительно оси z после перемещения дисков.
Перепишем уравнение (1) согласно введенным обозначениям:
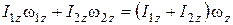 ,
,
откуда
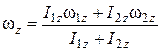 . (2)
. (2)
В выражении (2) 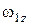 ,
, 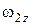 и
и 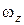 – величины алгебраические. Если диск вращается против часовой стрелки, то проекция вектора
– величины алгебраические. Если диск вращается против часовой стрелки, то проекция вектора  на ось z положительная
на ось z положительная 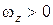 , если диск вращается по часовой стрелке, то проекция вектора
, если диск вращается по часовой стрелке, то проекция вектора  на ось z отрицательная
на ось z отрицательная  .
.
Приращение кинетической энергии вращения этой системы
 .
.
Заменив  его выражением (2), получим
его выражением (2), получим
 .
.
Знак минус показывает, что кинетическая энергия системы уменьшается.
Не нашли, что искали? Воспользуйтесь поиском: