Аналитический метод отделения корней

Аналитически корень уравнения можно определить, используя некоторые свойства функции, изучаемы в курсе математического анализа. Если в уравнении (7.1) функция 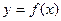непрерывная, то следует воспользоваться следующими известными фактами:

1 – Если на концах некоторого отрезка непрерывная функция принимает значения разных знаков, то на этом отрезке уравнение (7.1) имеет, по крайней мере, один корень.

2 – Если при этом функция имеет первую производную, не меняющую знака, то корень будет единственным.

3 – Пусть аналитическая функция 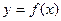на концах принимает значения разных знаков, т. е. 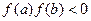, то между а и имеется нечетное число корней уравнения (7.1); если же на концах функция принимает значения одинаковых знаков, т. е. , то между а и или нет корней, или их имеется четное число (с учетом кратности);

Для непрерывной на отрезке функции можно предложить следующий порядок действий для отделения корней аналитическим методом:

1. Найти и определить критические точки.

2. Составить таблицу знаков функции , полагая х равным:

а) критическим значениям производных или ближайшим к ним;

б) граничным значениям области допустимых значений неизвестных.

3. Отделить интервалы, на концах которых функция принимает значения разных знаков. Внутри этих интервалов содержится по одному корню.

Пример.

, , , .

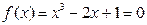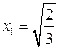x	-¥	-2	-1		+¥
	-	-	+	+	+

Данное уравнение имеет один корень, принадлежащий отрезку .

Не нашли, что искали? Воспользуйтесь поиском: