Экстраполяционная формула Ричардсона

Рассмотрим способ уточнения интегралов, основанный на приблизительном вычислении коэффициентов в разложении погрешности квадратурного правила.

Пусть погрешность имеет вид: , где – некоторая постоянная, подлежащая определению, 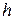– шаг интерполирования, m – показатель точности квадратурного правила, .

Пусть интеграл вычислен для значений и , где . Значит

Согласно предположению о структуре погрешности, имеем

где – точное значение интеграла, то для постоянной получим выражение:

и, следовательно, для погрешности: ,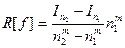

значит, в качестве уточненного значения интеграла можно взять выражение:

(6.13)

Указанный способ уточнения интегралов называют экстраполяцией по Ричардсону.На практике, в качестве можно брать значение 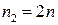, следовательно, формула (13) примет вид:

. (6.14)

Формула трапеций получается при .

Формула Ромберга

Последующее применение формулы Ричардсона позволяет уточнить значение интеграла.

Пусть известно, что для погрешности квадратурного правила справедливо разложение:

, (6.15)

где .

Будем считать, что приближенное значение вычисляется для последовательности шагов 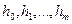, где .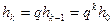

Обозначим , следовательно

. (6.16)

Рассмотрим (15) для двух соседних значений

;

Исключая 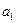имеем: .

Следовательно, в качестве уточненного значения можно взять:

. (6.17)

Описанный процесс можно продолжать, вычисляя по формулам:

. (6.18)

где , .

Заметим, что значение 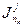совпадает с точным значением с погрешностью порядка .

Примерно к квадратурному правилу трапеции, описанный метод уточнения интегралов, называют методом Ромберга. Постоянные различные для квадратурного правила трапеции определяется формулой Эйлера.

Не нашли, что искали? Воспользуйтесь поиском: