Понятие о кубатурных формулах

Пусть необходимо приближенно вычислить кратный интеграл

Рассмотрим несколько способов построения формул численного интегрирования вида

(6.1)

Формулы (6.1) называются кубатурными формулами, а точки называются узлами кубатурной формулы.

Рассмотрим вычисление двойного интеграла. Пусть область интегрирования ограничена и непрерывна однозначными кривыми и двумя вертикалями .

Расставляя по известным правилам в двойном интеграле

(6.2)

пределы интегрирования будем иметь:

.

Рис. 1 Область интегрирования

Пусть

, (6.3)

тогда

. (6.4)

Применяя к однократному интегралу, стоящему в правой части равенства (6.4) одну из квадратурных формул, получим:

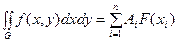, (6.5)

где , - некоторые постоянные коэффициенты.

В свою очередь могут быть найдены по известным квадратурным формулам: , где – соответствующие постоянные.

Из формулы (6.5) получаем, что

, (6.6)

где и – известные постоянные.

Геометрически этот метод приближен к вычислению объема I, выражаемого формулой (6.2) с помощью поперечных сечений. Для кубатурных формул (6.6) сохраняют силу соответствующих изменениям общие замечания, относящиеся к вычислению однократного интеграла.

Не нашли, что искали? Воспользуйтесь поиском: