Квадратурная формула Симпсона

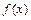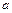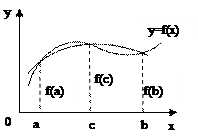
Пусть и интерполируется функция по трём точкам , , 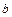в которых известны её значения. Интерполирующий многочлен имеет вторую степень и его графиком является парабола. Квадратурная формула парабол имеет вид

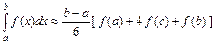. (5.15)

Это формула парабол. Она называется также формулой Симпсона. Формула точна для функции , так как левая и правая части формулы (5.15) тождественно равны нулю, а значит, она точна и для любого многочлена третьей степени.

Для нахождения погрешности формулы (5.15) рассмотрим многочлен 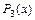третьей степени, удовлетворяющий условиям

.

Многочлен 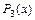интерполирует 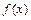по двум однократным узлам 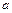и 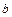и одному двукратному узлу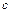

.

Так как для 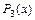формула Симпсона является точной, то

.

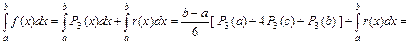
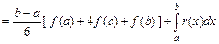Погрешность формулы Симпсона имеет вид

.

Если считать, что 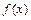имеет на отрезке непрерывную производную четвёртого порядка, то из представления остаточного члена интерполирования с кратными узлами, имеем

.

Поэтому

.

Так как множитель не изменяет знак на отрезке и – непрерывная функция на отрезке , то по теореме о среднем существует такая точка , что

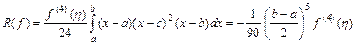. (5.16)

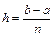Далее, разделим на чётное число равных частей длины и возьмём сдвоенный частичный отрезок . Тогда, учитывая, что , имеем

.

Просуммировав по всем сдвоенным отрезкам 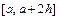, получим,

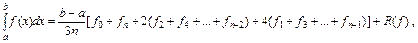
и

.

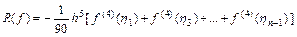Если функция непрерывна на отрезке , то существует такая точка , что

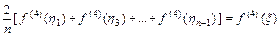
и для погрешности получим выражение

. (5.17)

Не нашли, что искали? Воспользуйтесь поиском: