
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Квадратурная формула трапеций
Для повышения точности интегрирования отрезок  часто делят на несколько частей, затем применяют избранную квадратурную формулу к каждой отдельной части и результаты складывают. Этот метод является общим, и им можно пользоваться при применении всякой квадратурной формулы. Для многих формул интерполяционных квадратур погрешность
часто делят на несколько частей, затем применяют избранную квадратурную формулу к каждой отдельной части и результаты складывают. Этот метод является общим, и им можно пользоваться при применении всякой квадратурной формулы. Для многих формул интерполяционных квадратур погрешность  зависит от величин отрезка интегрирования следующим образом
зависит от величин отрезка интегрирования следующим образом
 , (5.10)
, (5.10)
где  – медленно изменяющаяся функция от
– медленно изменяющаяся функция от 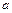 до
до 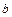 и
и  . Такая зависимость показывает, что если мы уменьшим отрезок интегрирования в
. Такая зависимость показывает, что если мы уменьшим отрезок интегрирования в 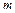 раз, то
раз, то  при этом уменьшится приблизительно в
при этом уменьшится приблизительно в  раз. Для вычисления интеграла по всему отрезку
раз. Для вычисления интеграла по всему отрезку  разделим его на
разделим его на 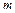 равных частей и вычислим при помощи выбранной формулы интегралы по всем частичным отрезкам. В каждом случае погрешность будет приблизительно в
равных частей и вычислим при помощи выбранной формулы интегралы по всем частичным отрезкам. В каждом случае погрешность будет приблизительно в  раз меньше, чем (5.10). При сложении всех таких интегралов получится результат, погрешность которого будет приблизительно в
раз меньше, чем (5.10). При сложении всех таких интегралов получится результат, погрешность которого будет приблизительно в  раз меньше, чем погрешность (10), когда формула применяется для вычисления интеграла по всему отрезку
раз меньше, чем погрешность (10), когда формула применяется для вычисления интеграла по всему отрезку  . Если
. Если 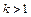 , то произойдёт уменьшение погрешности тем больше, чем больше
, то произойдёт уменьшение погрешности тем больше, чем больше  . Описанный способ увеличения точности применим сейчас к простейшим формулам Ньютона-Котеса.
. Описанный способ увеличения точности применим сейчас к простейшим формулам Ньютона-Котеса.
Пусть  , тогда линейное интерполирование выполняется по двум значениям
, тогда линейное интерполирование выполняется по двум значениям  и
и 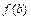 , принимаемым функцией
, принимаемым функцией 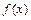 на концах
на концах 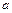 и
и 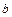 . Квадратурная формула (5.8), с учетом коэффициентов из таблицы, будет иметь вид
. Квадратурная формула (5.8), с учетом коэффициентов из таблицы, будет иметь вид
 (5.11)
(5.11)
Это формула трапеций.
Погрешность ее, в виду  и и  определяется по формуле определяется по формуле
|

 .
.
Если  – непрерывная функция на
– непрерывная функция на  , и так как множитель
, и так как множитель  сохраняет знак на
сохраняет знак на  , то по теореме о среднем, существует на
, то по теореме о среднем, существует на  такая точка
такая точка  , что
, что
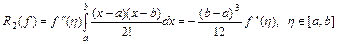 . (5.12)
. (5.12)
Для увеличения точности формулы трапеций (5.11), разделим отрезок  на
на  равных частей длины
равных частей длины 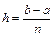 . Рассмотрим частичный отрезок
. Рассмотрим частичный отрезок  . Для него получим
. Для него получим
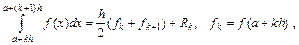
и согласно (5.12)
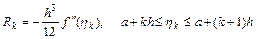 .
.

| Сумма интегралов по всем частичным отрезкам даёт общую квадратурную формулу трапеций |
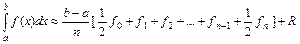 , (5.13)
, (5.13)
где

Величина  есть среднее арифметическое из значений второй производной. Считая ее непрерывной функцией на
есть среднее арифметическое из значений второй производной. Считая ее непрерывной функцией на  , мы можем выбрать такую точку
, мы можем выбрать такую точку  , что
, что
 ,
,
а значит, величина погрешности может быть определена по формуле
 . (5.14)
. (5.14)
Не нашли, что искали? Воспользуйтесь поиском: