Лекция 5 Численное интегрирование

1 Постановка задачи.

2 Квадратурная формула трапеций.

3 Квадратурная формула Симпсона.

Постановка задачи

Пусть – любой отрезок числовой оси, и рассматривается интеграл . Ставится задача: найти его приближённое значение по значениям функции в точках . Формулы для вычисления интегралов называют квадратурными.

Многие правила приближённых квадратур основаны на замене интегрируемой функции на всём отрезке или на его частях на более простую функцию 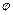, близкую к , легко интегрируемую точно и принимающую в узлах те же значения , что и . В качестве такой функции берут алгебраический или тригонометрический многочлен, либо дробно-рациональную функцию.

Когда отрезок интегрирования конечный и интегрируемая функция имеет высокую гладкость, то можно рассчитывать хорошо приблизить её многочленом невысокой степени. Если же сама функция или её производные невысоких порядков имеют особенности или даже обращаются в 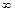, то это затруднит приближение или сделает его вообще невозможным. В этом случае мы должны будем заранее освободиться от таких особенностей путём их выделения. Делается это при помощи разложения на два сомножителя , где имеет такие же особенности, как и 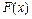, а 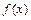– есть достаточно гладкая функция, и интеграл рассматривается в форме .

Функция называется весовой функцией или весом. При построении определённого квадратурного правила она считается фиксированной.

Будем строить приближённые формулы вычислений вида

, . (5.1)

Числа 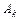называются квадратурными коэффициентами, 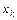– квадратурными узлами, а правая часть формулы – квадратурной суммой.

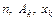
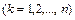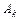Формула (5.1) содержит параметров: . Их следует выбирать так, чтобы (5.1) давала, возможно, лучший результат при интегрировании избранного класса функций . Роль – очевидна: чем больше , тем больше слагаемых в квадратурной сумме, и тем большей точности можно достичь путём выбора и 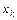. Поэтому при построении формулы число считают фиксированным и рассматривают задачу о выборе 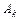и 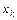. В различных квадратурных методах одно из множеств: либо множество коэффициентов 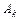, либо множество узлов 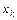также может быть зафиксированным. Правом выбора их обычно пользуются для следующих целей:

– Увеличение степени точности

Говорят, что квадратурная формула (5.1) имеет степень точности 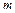, если она является точной для функций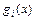 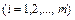, т.е.

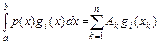
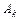и не является точной для . Можно стремиться к тому, чтобы при помощи выбора параметров и 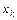сделать степень точности формулы (5.1) наивысшей возможной. Такие формулы впервые были рассмотрены Гауссом и их часто называют формулами наивысшей степени точности.

– Минимизация погрешности

Остаточный член формулы (1) имеет вид

. (5.2)

За величину, характеризующую точность формулы на множестве функций может быть принята

.

Путём выбора узлов 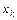и коэффициентов 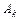можно добиться, чтобы величина имела бы наименьшее значение.

– Упрощение вычислений

Можно при помощи выбора параметров 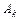и 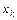стремиться сделать, возможно, более простыми вычисления по формуле (5.1), например, взять равноотстоящими узлы, или взять равные коэффициенты.

Не нашли, что искали? Воспользуйтесь поиском: