Точечный метод наименьших квадратов

Пусть на отрезке задана система точек . При точечном квадратичном аппроксимировании за меру отклонения алгебраического полинома от функции 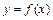на данном множестве точек берут величину

, (4.4)

которая называется квадратичным отклонением.

Полином следует строить таким образом, чтобы величина этого отклонения была минимальной. Если , то в качестве можно взять интерполяционный полином Лагранжа , так как для него величина среднеквадратичного отклонения равна нулю

.

Если 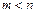, то для минимизации отклонения необходимо решить систему

.

Таким образом, для определения минимизации функции квадратичного отклонения необходимо взять частные производные от величины , по всем переменным . Приравнивая эти частные производные к нулю, получим систему m +1 уравнений с m +1 неизвестными :

. (4.5)

Для удобства вычисления введем обозначения:

и , k=0,1,2…

Тогда система (4.5) может быть записана в виде:

. (4.6)

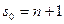
Если среди точек нет совпадающих, то определитель системы неравен нулю. То есть система уравнений (4.6) совместна и из решения этой системы определяем неизвестные коэффициенты . Полином с такими коэффициентами будет обладать минимальным отклонением. Так как матрица системы (4.6) положительно определена, и для ее решения можно использовать любой численный метод, например, Зейделя или метод простой итерации.

Для удобства формирования и решения системы (4.6) промежуточные результаты рекомендуется записывать в следующей таблице.

Таблица 1. Коэффициенты системы

	xi	yi
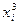
1	x0	y0
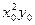
1	x1	y1
1	x2	y2
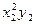
1	x3	y3
1	x4	y4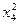
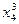
S0	S1	t 0	S2	S3	S4	t 1	t 2

Не нашли, что искали? Воспользуйтесь поиском: