Численное дифференцирование

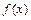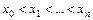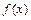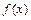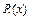Пусть на отрезке рассматривается функция , имеющая непрерывную производную порядка . Возьмем на различный узел (для удобства) и известны значения функции в них . Требуется найти значение -ой производной от функции в любой точке . Построим интерполяционный многочлен для функции степени с погрешностью . Тогда запишем . Для производной порядка имеем . Если погрешность мала, то пренебрегая ею, получим формулу для приближенного вычисления производной 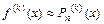. Пользоваться этой формулой целесообразно при небольших порядках , когда , так как все производные от порядка выше тождественно равны нулю.

Получим некоторые явные формулы для численного вычисления производных при некоторых видах .

Не нашли, что искали? Воспользуйтесь поиском: