Интерполяционные формулы Ньютона для равноотстоящих узлов

Пусть на отрезке заданы 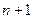значений , в которых известны значения некоторой функции 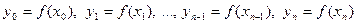. Требуется найти полином степени не выше , такой, чтобы выполнялось условие

. (2.1)

Теорема 1.1 Существует и при том единственный многочлен степени не выше , для которого выполняется условие (2.1).

Доказательство. Пусть многочлен имеет вид:

.

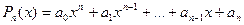Используя формулы (2.1), для определения коэффициентов , получим следующую систему линейных алгебраических уравнений:

. (2.2)

Определителем системы (2.2) является определитель Вандермонда. Он имеет вид

.

Следовательно, для системы различных между собой узлов система (2.2) имеет единственное решение. Теорема доказана.

Очевидно, что условие (2.1) эквивалентно условию

. (2.3)

Будем искать интерполяционный полином в виде

(2.4)

Из (2.4) при сразу получим . Найдем первую конечную разность

.

Применяя (2.3), для коэффициента получим выражение . Аналогично, учитывая (2.3), для второй конечной разности справедлива формула и, следовательно, .

Продолжая наши рассуждения, запишем формулу для любого : . Подставляя в (2.4) выражения для коэффициентов через конечные разности, получим первую интерполяционную формулу Ньютона

. (2.5)

Для практических целей формулу Ньютона (2.5) удобнее записывать в несколько ином виде. Введем переменную . Тогда . Таким образом, для полинома получим выражение

. (2.6)

Формулу (2.6) выгодно использовать для интерполирования в окрестности начального значения . Поэтому ее часто называют формулой для интерполирования вперед. В этой формуле из таблицы конечных разностей используются верхней диагонали.

Остаточный член в формуле (2.6) имеет вид

,

где – некоторая внутренняя точка наименьшего промежутка, содержащего все узлы и точку . При наличии дополнительного узла 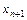на практике пользуются более удобной приближенной формулой

. (2.7)

При из (2.6) получается формула линейного интерполирования

.

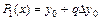При из (2.6) имеет место формула параболического или квадратического интерполирования

.

Первая интерполяционная формула Ньютона практически неудобна для интерполирования функций в конце таблицы. Поэтому когда точка интерполирования лежит вблизи точки удобно пользоваться второй интерполяционной формулой Ньютона, которая имеет вид

. (2.8)

Вводя новую переменную , эту формулу перепишем в виде

(2.9)

В формуле (2.9) из таблицы конечных разностей используются нижней диагонали.

Остаточный член формулы (2.9) имеет вид

, (2.10)

где точка имеет тот же смысл, что и ранее.

Отметим, что формулы Ньютона используются и для экстраполирования функций. Если , то для экстраполирования назад используют первую интерполяционную формулу Ньютона. Если , то для экстраполирования вперед используют вторую интерполяционную формулу Ньютона. Следует заметить, что операция экстраполирования менее точна, чем операция интерполирования в узком смысле.

Не нашли, что искали? Воспользуйтесь поиском: