
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Интерполяционная формула Лагранжа. Построим формулу для произвольного расположения узлов интерполирования
Построим формулу для произвольного расположения узлов интерполирования. Пусть на отрезке  заданы
заданы 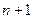 значений
значений  , в которых известны значения некоторой функции
, в которых известны значения некоторой функции 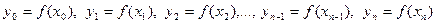 . Построим полином
. Построим полином 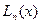 , для которого выполняются равенства
, для которого выполняются равенства
 . (1.5)
. (1.5)
Решим сначала вспомогательную задачу и построим полином 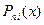 степени
степени  , удовлетворяющий условию
, удовлетворяющий условию
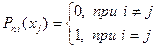 . (1.6)
. (1.6)
Из условия (1.6) следует, что полином 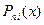 имеет
имеет  корней в узлах
корней в узлах  . Следовательно, он может быть записан в виде
. Следовательно, он может быть записан в виде
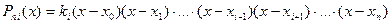 .
.
Так как 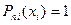 , то для
, то для  получим выражение
получим выражение
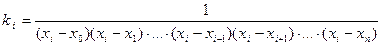 . (1.7)
. (1.7)
Очевидно, что тогда полином 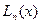 можно записать в виде
можно записать в виде
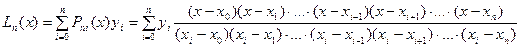 . (1.8)
. (1.8)
Формула (1.8) называется интерполяционной формулой Лагранжа.
Обычно формулу Лагранжа записывают в другом виде. Рассмотрим полином  степени
степени 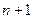
 .
.
Для первой производной справедливо выражение
 .
.
С учетом введенных обозначений полином Лагранжа можно записать в виде
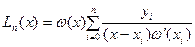 . (1.9)
. (1.9)
Пример
Построить полином Лагранжа для функции заданной таблично:
| I | ||||
| X | ||||
| Y |
Из таблицы видно, что полином Лагранжа третьей, так как n=3.
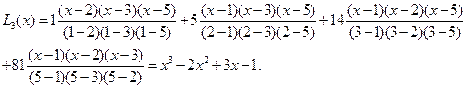
Проверка: 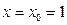 ,
, 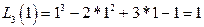 ,
,  .
.
Не нашли, что искали? Воспользуйтесь поиском: