Постановка задачи интерполирования

ПРИБЛИЖЕНИЕ ФУНКЦИЙ

Лекция 1 Многочлен Лагранжа

1 Постановка задачи интерполирования.

2 Примеры интерполяционных функций.

3 Интерполяционная формула Лагранжа.

В экономике, физике представление результатов в большинстве случаев задается в виде табличной зависимости, что не всегда удобно для всестороннего анализа. Поэтому возникает задача о получении аналитической зависимости по табличному представлению функции или задач о приближении функции, или задача интерполировании.

Постановка задачи интерполирования

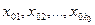Рассмотрим на отрезке некоторую – кратно дифференцируемую функцию . Пусть в точках известны ее значения , в точках известны значения первой производной , и в 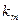точках известны значения -ой производной . Значения функции и ее производных называются данными интерполирования, а точки – узлами интерполирования.

Задача интерполирования заключается в отыскании функции из некоторого класса такой, что выполняется условие

. (1.1)

Пусть . Рассмотрим на отрезке последовательность линейно независимых – кратно дифференцируемых функций:

.

В качестве семейства возьмем всевозможные линейные комбинации первых функций с произвольными коэффициентами:

.

Из условия (1.1) получим систему линейных алгебраических уравнений для определения коэффициентов :

. (1.2)

Система (1.2) будет иметь единственное решение в том случае, если ее определитель отличен от нуля.

Не нашли, что искали? Воспользуйтесь поиском: