Конечные разности и их свойства

Пусть некоторое фиксированное приращение аргумента функции 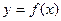. Величина называется первой конечной разностью функции 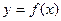в точке . Конечной разностью порядка называется конечная разность первого порядка от конечной разности порядка. Так, например, конечную разность второго порядка можно записать

.

Если , то его первая конечная разность имеет вид

и, следовательно, являются полиномом порядка . Можно показать, что

и .

Из определения конечных разностей вытекают следующие свойства:

1) ,

2) ,

3) .

Докажем, например, свойство 3): .

Конечные разности обычно располагают в таблице.

Таблица 1.1 Конечные разности

x
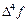
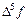
x0	f0
x1	f1
x2	f2
x3	f3
x4	f4
x5	f5
x6	f6

Лемма 1.1 Пусть функция имеет непрерывную производную порядка на отрезке . Тогда справедлива формула

.

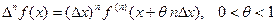Доказательство проведем по индукции. При получим формулу конечных приращений Лагранжа . Пусть наше утверждение справедливо при :

. Тогда для , получим

.

Лемма доказана.

Предполагая, что непрерывна на отрезке и переходя к пределу при , получим

.

Не нашли, что искали? Воспользуйтесь поиском: