Обратная задача интерполирования

Часто на практике возникает задача об отыскании по заданному значению функции значения аргумента. Эта задача решается методом обратного интерполирования.

Если заданная функция монотонна, то обратное интерполирование проще всего осуществить путем замены функции аргументом и обратно, и последующего интерполирования.

Если заданная функция не монотонна, то этим приемом воспользоваться нельзя. Тогда не меняя ролями функцию и аргумент, записываем ту или иную интерполяционную формулу, используя известные значения аргумента и считая функцию известной, решаем полученное уравнение относительно аргумента.

Пусть на отрезке заданы узлы интерполирования и известны соответствующие значения . Теперь необходимо по заданному значению функции определить аргумент , соответствующий этому значению. Для произвольной функции задача обратного интерполирования не может быть решена однозначно. Решение будет однозначным, если функция 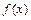монотонна на минимальном отрезке, содержащем узлы интерполирования.

Рассмотрим два случая.

Если узлы интерполирования равноотстоящие, то для решения поставленной задачи можно использовать метод последовательных приближений, который заключается в следующем. Пусть функция 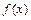монотонна и значение содержится между и 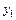. Запишем первую интерполяционную формулу Ньютона (2.6)

.

Перепишем ее в виде

. (3.1)

Для отыскания можно использовать итерационный процесс

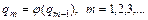. (3.2)

В качестве нулевого приближения можно взять 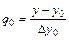. Для достаточно гладких функций при малом шаге итерационный процесс (3.2) сходится. Если 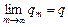, то значение искомого аргумента определяется из формулы .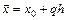

В случае неравноотстоящих узлов значение аргумента можно определить по формуле Лагранжа для обратной функции

. (3.3)

Не нашли, что искали? Воспользуйтесь поиском: