Погрешность формул численного дифференцирования

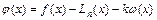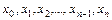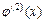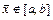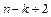Рассмотрим сначала случай, когда точка не принадлежит минимальному отрезку , содержащему узлы интерполирования. Введем вспомогательную функцию . Функция имеет нулей в точках по построению. На основании теоремы Ролля будет иметь , – и будет иметь нулей внутри отрезка . Выберем теперь таким, чтобы также являлась корнем . Так как , то это всегда можно сделать, полагая . Тогда будет иметь нулей и, следовательно, обращается в нуль, по крайней мере, в одной точке . Получим . Подставляя выражение для в последнее равенство, получим выражение для погрешности дифференцирования

. (3.11)

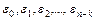Пусть и . Разность обращается на отрезке в нуль в точках . Будем считать, что 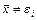, и рассмотрим функцию

.

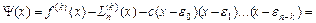
Если 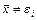, то константу 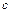можно подобрать так, чтобы . Используя последнее условие, получим . При указанном выборе 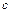функция будет иметь нулей и , по крайней мере, обращается в нуль в одной точке . То есть . Подставляя выражение для 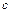в последнее равенство, получим

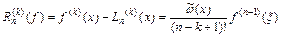. (3.12)

Заметим, что при использовании формул численного дифференцирования может произойти существенная потеря точности. Поясним это на простом примере.

Пусть вычисляется по формуле . Если , то погрешность формулы будет . Допустим, что значения функции и 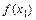вычисляются с погрешностью . В этом случае появится дополнительная погрешность 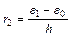и .

Величина общей погрешности удовлетворяет неравенству

.

Определим минимум : . Отсюда определим и . Если , где 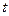разрядность сетки ЭВМ, то из оценки следует, что в лучшем случае вычисляется с половиной верных разрядов.

Не нашли, что искали? Воспользуйтесь поиском: