Интегральный метод наименьших квадратов

Пусть задана система фундаментальных функций:

,

тогда полином запишется в виде

, (4.7)

Для случая точного метода минимизируем , в случае интегрального метода минимизируем . Определим коэффициенты разложения из условия . Дифференцируя , получим систему

.

Таким образом, получим систему алгебраических уравнений

. (4.8)

Здесь выражение и представляют собой скалярные произведения и соответственно равны.

Для точечного метода

, (4.9)

где , , если функция задана таблично.

Для интегрального метода, если функция 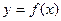задана аналитически на отрезке скалярные произведения определяются

. (4.10)

Если система фундаментальных функций ортогональна, т.е. , то для вычисления коэффициента из системы уравнений (4.8) сразу можно записать

, (4.11)

если же система фундаментальных функций ортонормированна, то

. (4.12)

Полученные таким образом коэффициенты называется коэффициентами Фурье для приближенных функций 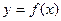тригонометрический полином.

Так как система функций

ортогональна, то приближение функций тригонометрическим полиномом можно производить, используя метод наименьших квадратов для функции заданной аналитически.

Пример. Пусть задана функция на требуется построить аппроксимирующий многочлен степени он имеет вид:

,где , ,

Так как скалярное произведение , то для определения скалярного произведения с разными индексами имеем:

, ,

, ,

,

,

В результате получаем систему (4.8).

Контроль правильности вычисления:

1. прежде всего, после решения системы уравнений необходимо подставить коэффициенты в уравнения системы (4.8) и проверить, совпадает ли правая часть с левой;

2. так как аппроксимирующий многочлен не совпадает со значением функции на заданном множестве точек, то следует вычислять по формуле (4.1) величину для точечного метода наименьших квадратов или по формуле (4.2) для интегрального метода наименьших квадратов и если после подстановки в многочлены значения x, где известно значение функции отклонение между ними не будет превосходить величину , то аппроксимирующий многочлен построен правильно.

Не нашли, что искали? Воспользуйтесь поиском: