Формулы Ньютона-Котеса

В вычислениях часто узлы 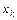берутся равноотстоящими. Построим интерполяционные квадратурные формулы, считая, что на отрезке задано равноотстоящих узлов 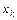, таких, что , , и 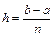. Введем новую переменную 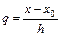. Тогда многочлен Лагранжа примет вид

.

Подставим это выражение в (5.3), получим

.

Полученную формулу перепишем в виде

, (5.6)

где

(5.7)

Квадратурные правила (5.6) называют формулами Ньютона-Котеса, а коэффициенты (5.7) – коэффициентами Ньютона-Котеса.

Для постоянной весовой функции формула Ньютона-Котеса имеет вид

, (5.8)

а коэффициенты определяются по формулам

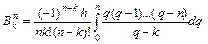. (5.9)

Нетрудно видеть, что для коэффициентов справедливы соотношения и , например, последнее легко показывается с помощью замены .

Коэффициенты вычислены до . Однако для больших значений формулы Ньютона-Котеса не применяются, так как с ростом все значительнее сказывается неустранимая и вычислительная погрешность. В следующей таблице приведем некоторые значения коэффициентов

Таблица 5.1 Значение коэффициентов

Например, .

Замечание. Формула (5.9) имеет степень точности , если число узлов её – является чётным, и степень , если число узлов её – является нечётным.

Не нашли, что искали? Воспользуйтесь поиском: