Среднеквадратичные приближения функций

На практике часто бывает необходимо построить аппроксимирующий многочлен степени , где n -множество точек на котором заданна функция 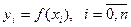. Так как, в этом случае, интерполирование невозможно, то прибегают к другим приемам, позволяющим получить приближение функций. Обычно используют метод наименьших квадратов.

Уточним понятие квадратичного отклонения. Для этого введем соответствующее расстояние между данной непрерывной функцией и полиномом – так называемое среднеквадратичное отклонение.

Определение 1. Под средним квадратичным отклонением функции и полинома на множестве точек понимается число

. (4.1)

В этом случае аппроксимация называется точечной.

Если функция заданна аналитически, тогда аппроксимация называется интегральной, и среднеквадратичное отклонение на отрезке определяется формулой:

. (4.2)

Формулу (4.2) можно рассмотреть как предельный случай формулы (1) при . Если среднее квадратичное отклонение мало, то для большинства значений x из абсолютная величина также мала при . Следовательно , где .

Рис. 1 Приближение функции

Такая ситуация наблюдается в ряде случаев при обработке результатов наблюдений и с помощью приближения функции мы можем получить закон изменения этих результатов.

Во многих случаях, например, при обработке результатов эксперимента оно сглаживает отдельные локальные неровности. Однако иногда для приближения функций ставят более жесткие условия: требуется гарантировать, чтобы отклонение на отрезке и было меньше заданной величины, то есть равно величине абсолютного отклонения.

Определение 2. Абсолютным отклонением на отрезке обобщенного полинома от непрерывной функции называется число

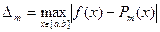. (4.3)

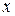Если , то из формулы (4.3) следует, что для всех точек на отрезке . Тогда говорят, что обобщенный полином на отрезке равномерно приближает функцию с заданной точностью . Для случая алгебраических многочленов справедлива теорема Вейерштрасса.

Теорема Вейерштрасса. Если функция непрерывна на то, как бы мало ни было положительное число , найдется полином достаточно высокой степени абсолютное отклонение которого от данной функции на не меньше , то есть для любого имеет место неравенство: .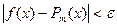

Не нашли, что искали? Воспользуйтесь поиском: