Первая и вторая интерполяционные формулы Ньютона

Покажем, что, используя понятие разностных отношений, формулу Лагранжа можно записать в виде аналогичном первой и второй интерполяционным формулам Ньютона для равноотстоящих узлов. Пусть полином Лагранжа, для которого выполняется условие

. (2.22)

Тогда и . По определению, для второго разностного отношения имеем

.

Откуда . Последовательно выражая разностные отношения 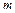-го порядка через отношения -го порядка по формуле

,

окончательно для полинома получим представление

Учитывая (2.22) и то, что , получим первую интерполяционную формулу Ньютона для неравноотстоящих узлов

. (2.23)

Аналогичным образом можно построить и вторую интерполяционную формулу Ньютона для неравноотстоящих узлов, которая имеет вид

. (2.24)

Кроме формул (1.12) и (1.14) для оценки погрешности получим еще одну исходя из формулы Ньютона. Добавим к узлам 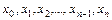еще один узел , то есть точку, в которой вычисляется значение функции 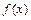. Тогда по формуле выражающей значения функции в узле через начальные разностные отношения, получим

Заметим, что в правой части сумма всех слагаемых без последнего интерполяционной формулой Ньютона (2.23). Тогда

,

или

. (2.25)

Сравнивая формулы (1.12) и (2.25) получим, что

.

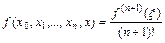Для вычисления погрешности можно пользоваться формулами (1.12), (1.14), (1.15).

Не нашли, что искали? Воспользуйтесь поиском: