Разностные отношения и их свойства

В том случае, когда значения аргумента являются неравноотстоящими для исследования и вычисления функции используются разностные отношения (разделенные разности). Пусть на отрезке заданы произвольные попарно различные узлы интерполирования , в которых известны значения некоторой функции : .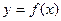

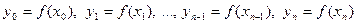Разностными отношениями первого порядка называются величины

. (2.11)

По разностным отношениям первого порядка составляются разностные отношения второго порядка

(2.12)

Разностные отношения любого порядка определяются при помощи разностных отношений предыдущего порядка по формуле

. (2.13)

Используя определение, можно показать, что разностное отношение является симметрической функцией своих аргументов так, что выполняется равенство

. (2.14)

Лемма 1. Если полином степени , то его конечная разность порядка равна нулю для любой системы попарно различных между собой чисел

. (2.15)

Доказательство. Так как полином имеет корень в точке , по определению, получим

.

С учетом (2.12) полином обращается в нуль в точке и вторая конечная разность будет полиномом степени

.

Продолжая аналогичные рассуждения, приходим к выводу, что

и, следовательно, для разностного отношения порядка справедливо равенство (2.15). Лемма доказана.

Теперь получим выражения разностных отношений всех порядков через значения функции. Из определения разностного отношения первого порядка имеем

. (2.16)

Для разностного отношения второго порядка получим

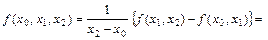
(2.17)

Приведем еще выражение любого значения функции через начальное значение и разностные отношения для начальной точки . Из определения вытекает равенство

. (2.18)

На основании соотношений (2.18) и (2.17) будем иметь

Используя индукцию, получим

(2.19)

Отметим некоторые свойства разностных отношений

1. Свойство аддитивности. Если , то .

1. Свойство подобия. Если , где , то .
2. Свойство симметрии. Разностное отношение 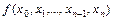есть симметричная функция своих аргументов (см. (2.14)).

4. Если есть многочлен степени , то разностное отношение -го порядка не зависит от и равняется коэффициенту при старшей степени в многочлене . Все разностные отношения порядка большего равны нулю (см. лемму 1).

Установим связь между разностными отношениями и конечными разностями. Предположим, что значения аргумента являются равноотстоящими . Тогда получим

(2.20)

Для разностного отношения второго порядка имеем

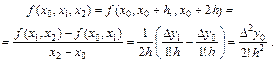
И для -го разностного отношения имеет место равенство

. (2.21)

Не нашли, что искали? Воспользуйтесь поиском: