Оценка погрешности формулы Лагранжа

Проводя интерполирование по формуле (1.9) или (1.8), мы допускаем некоторую погрешность

,

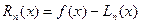которая является нулевой в общем случае только в узлах интерполирования. Будем считать, что на отрезке интерполирования функция имеет все производные вплоть до 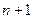порядка включительно. Рассмотрим вспомогательную функцию

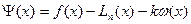. (1.10)

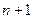Очевидно, что имеет корней в узлах . Выберем произвольную точку 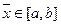и подберем постоянную так, чтобы выполнялось равенство

.

Отсюда

. (1.11)

При таком выборе имеет корня на и обращается в 0 на концах отрезков . Следовательно, по теореме Роля имеет 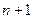корень на отрезке , имеет корней, и – имеет по крайней мере один корень на отрезке в некоторой точке . То есть

.

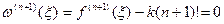Подставляя из последнего выражения в (1.11), получим выражение для погрешности интерполирования

, (1.12)

где точка . Этой формулой можно воспользоваться, если функция задана аналитически. В случае если функция задана таблично на системе равностоящих точек , , то при достаточно малом шаге , производную можно приближенно заменить конечно-разностным отношением

,

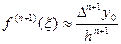где 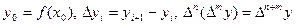– конечные разности. Тогда остаточный член примет вид

. (1.13)

Если известна постоянная 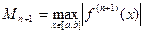, то для погрешности интерполирования по формуле Лагранжа можно воспользоваться оценкой

. (1.14)

Имеется и более точная формула для определения погрешности

(1.15)

Не нашли, что искали? Воспользуйтесь поиском: