Методы уточнения интегралов

В тех случаях, когда известно разложение погрешности квадратичной формулы в степенной ряд по 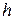приблизительное значение интеграла можно уточнить, проводя точное вычисление коэффициентов ряда.

Формула Эйлера

Рассмотрим функцию . Возьмем ее разложение в равном сходящемся по 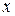ряд при 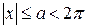. Запишем 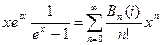, где коэффициенты 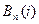ряда называют многочленами Бернулли, а их значения при 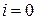– числом Бернулли,

= , .

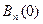Значение чисел Бернулли можно получить используя рекуррентную формулу для чисел Бернулли:

.

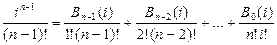Пусть 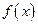достаточно гладкая на функция, тогда можно показать, что имеет место формула:

.

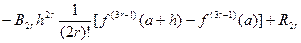После суммирования по всем получаем:

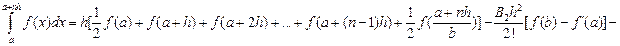
. (6.12)

Формула (6.12) называется формулой Эйлера. Она позволяет уточнить значение интеграла, вычисляя по формуле трапеции путем вычисления производных от подынтегральной функции на концах отрезка.

Не нашли, что искали? Воспользуйтесь поиском: