
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Определение числа действительных корней
Пусть дано алгебраическое уравнение  степени
степени
 , (7.3)
, (7.3)
где 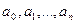 – действительные коэффициенты.
– действительные коэффициенты.
Определить приближенно число действительных корней уравнения (7.3) можно с помощью правила Декарта: Число положительных корней уравнения (7.3) с учетом их кратностей равно числу перемен знаков в последовательности коэффициентов 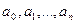 (причем равные нулю коэффициенты не учитываются) или меньше этого числа на четное число. Для определения числа отрицательных корней достаточно применить правило Декарта к многочлену
(причем равные нулю коэффициенты не учитываются) или меньше этого числа на четное число. Для определения числа отрицательных корней достаточно применить правило Декарта к многочлену  .
.
Более точно число корней уравнения (7.3) можно определить, используя теорему Штурма: Пусть уравнение (3) не имеет кратных корней на некотором отрезке  . Обозначим через
. Обозначим через  производную
производную  ; через
; через  остаток от деления
остаток от деления  на
на  , взятый с обратным знаком; через
, взятый с обратным знаком; через  остаток от деления
остаток от деления  на
на  , взятый с обратным знаком; и т.д. до тех пор, пока не получим
, взятый с обратным знаком; и т.д. до тех пор, пока не получим  . Получился так называемый ряд Штурма:
. Получился так называемый ряд Штурма:
 . (7.4)
. (7.4)
Число действительных корней уравнения (7.3), расположенных на отрезке  , равно разности между числом перемен знаков в последовательности (7.4) при
, равно разности между числом перемен знаков в последовательности (7.4) при  и числом перемен знаков в последовательности (7.) при
и числом перемен знаков в последовательности (7.) при  .
.
Практическое применение теоремы Штурма сводится к следующему: Определяются границы отрезка, на котором расположены действительные корни уравнения (7.3) и их число. Полученный отрезок  делится на некоторое число частей точками
делится на некоторое число частей точками 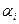 :
:  . Рассматривая отрезок
. Рассматривая отрезок 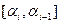 по теореме Штурма, определяется число корней на этом отрезке. Если окажется, что их больше одного, то этот отрезок делится пополам и теорема Штурма применяется к каждому полученному отрезку. Процесс продолжается до тех пор, пока на каждой части отрезка
по теореме Штурма, определяется число корней на этом отрезке. Если окажется, что их больше одного, то этот отрезок делится пополам и теорема Штурма применяется к каждому полученному отрезку. Процесс продолжается до тех пор, пока на каждой части отрезка  уравнение (7.3) будет иметь не больше одного действительного корня.
уравнение (7.3) будет иметь не больше одного действительного корня.
Пример. Отделить корни уравнения
 .
.
Находим выражения:  ,
, 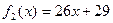 ,
,  . Составляем таблицу.
. Составляем таблицу.

| 
| 
| |||

| - | - | - | + | + |

| + | - | + | + | + |

| - | + | + | + | + |

| - | - | - | - | - |
| Число перемен знаков |
Из таблицы видно, что действительный корень один и находится он в интервале  .
.
Не нашли, что искали? Воспользуйтесь поиском: