Методы итераций, хорд и Ньютона

Все методы уточнения основаны на последующем приближении. Обычно используют метод: итераций, хорд, Ньютона, комбинаторный.

Метод итераций

Уравнение (7.1) заменяется равносильным ему уравнением

. (7.5)

Допустим, нам известно некоторое начальное приближение . Тогда, в простейшем методе итераций, все дальнейшие приближения строятся по формуле

. (7.6)

Если последовательность (7.6) сходится при некотором выборе начального приближения , то существует предел и предполагая функцию непрерывной, найдем

или . Таким образом, является корнем уравнения (7.5) и может быть вычислен по формуле (7.6) с любой степенью точности.

Геометрически способ итерации может быть пояснен следующим образом. Построим на плоскости графики функций и . Каждый действительный корень уравнения (7.5) является абсциссой точки пересечения кривой с прямой . Следующие два рисунка поясняют сходящийся итерационный процесс (Рис.3, Рис. 4).

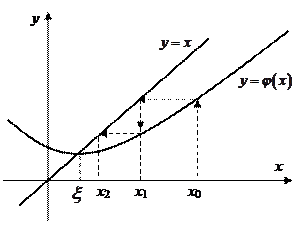
Рис. 3 Сходящийся процесс при

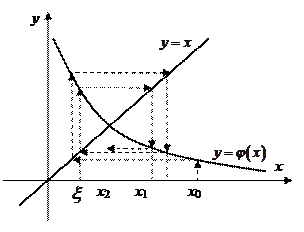
Рис. 3 Сходящийся процесс при , но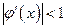

На рисунках 5 и 6 схематично изображен расходящийся итерационный процесс.

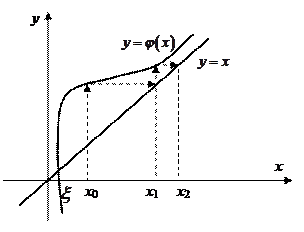
Рис. 5 Расходящийся процесс при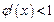

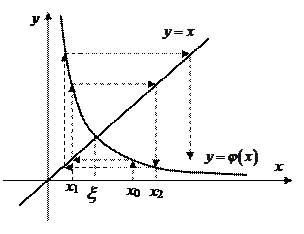
Рис. 6 Расходящийся процесс при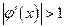

Поэтому для практического применения метода итерации нужно выяснить достаточные условия сходимости итерационного процесса.

Теорема: Пусть определена и дифференцируема на и все её значения принадлежат отрезку . Если существует такое q, что

, (7.7)

то итерационный процесс (7.6) сходится к единственному корню на .

Для скорости сходимости итерационного процесса, справедливы соотношения

(7.8)

(7.9)

. (7.10)

Из (7.8) следует, что метод сходится со скоростью геометрической прогрессии со знаменателем q. Формула (7.9) позволяет определить достаточное число итераций при выбранном . На практике для оценки сходимости удобно пользоваться (7.10). Так, если , то корни уравнения определяются с точностью до .

Обычно для получения пользуются следующим способом приведения (7.1) к виду (7.5). Строят уравнение

(7.11)

где – параметр. Пусть постоянного знака на отрезке . Для нахождения положим

l= , ,

В этом случае будет верно , значит итерационный процесс по формуле (7.11) будет сходящимся.

2.2 Метод хорд

Пусть дано уравнение (7.1) с непрерывными на отрезке функцией и ее производными . Корень считается отделённым на и притом единственным.

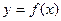Рассмотрим случай, когда – одного знака. Пусть для определенности , , т.е. . График функции проходит через точки , (Рис. 8).

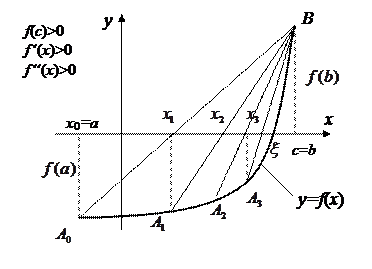
Рис. 8 Иллюстрация метода хорд

Искомый корень уравнения – есть абсцисса пересечения графика с осью OX. Эта точка нам известна, но вместо нее можно взять точку – точку пересечения хорды с осью OX. Это и будет первое приближение к корню . Уравнение хорды, проходящей через две точки и В, запишется:

.

Положив , найдем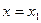

.

Однако последовательные приближения при этом можно вычислить по следующей итерационной формуле:

. (7.12)

В формуле (7.12) точка является неподвижной и в качестве ее берется тот конец , для которого выполняется условие 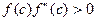, а за начальное приближение выбирается противоположный конец , так что (в нашем случае ).

Описанный метод называется также методом секущих или методом линейной интерполяции. Последовательные приближения в методе хорд образуют – монотонную, ограниченную сверху или снизу корнем последовательность. При этом справедлива оценка:

, (7.13)

где , . Оценка (7.13) позволяет на каждом шаге следить за достигнутой точностью.

При решении задачи на ЭВМ целесообразно выбирать столь малым, чтобы выполнялось условие . В этом случае итерационный процесс сходится быстро.

Метод хорд (секущих) можно рассматривать, как метод итерации для эквивалентного уравнения:

, где .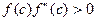

Геометрически этот метод состоит в том, что значение есть абсцисса точки пересечения прямой, проходящей через точк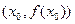и и с осью Ох. Графическая иллюстрация метода приведена на рисунках 8-11.

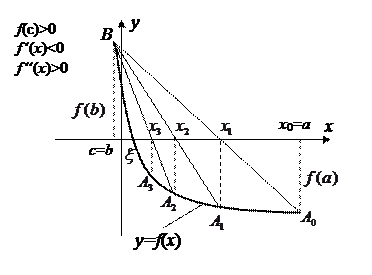
Рис. 9 Иллюстрация метода хорд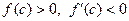

Рис. 10 Иллюстрация метода хорд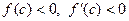

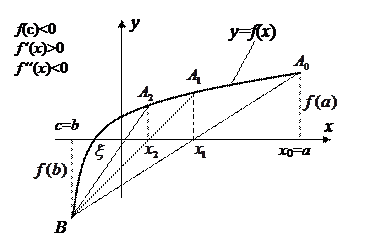
Рис. 11 Иллюстрация метода хорд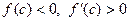

Из приведенного выше следует, что выбор неподвижной точки осуществляется следующим образом:

1 – неподвижен тот конец отрезка, для которого знак функции совпадает со знаком ее второй производной .

2 – последовательные приближения лежат по ту сторону корня , где функция имеет знак, противоположный знаку ее второй производной .

В обоих случаях каждое следующее приближение ближе к корню , чем предшествующее .

Метод Ньютона

Метод Ньютона (касательных) позволяет привести решение нелинейных уравнений к решению последовательности линейных задач. Достигается это при помощи выделения из нелинейного уравнения его главной линейной части.

Пусть корень уравнения (7.1) отделен на , причем непрерывны и сохраняют определенные знаки и не обращается в нуль на . Метод Ньютона заключается в том, что кривая уравнения 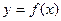заменяется касательной к ней. Имея -ое приближение корня , уточним его по методу Ньютона следующим образом: положим

, (7.14)

где считаем малой величиной. Теперь, применяя формулу Тейлора, получим

.

Откуда следует, что

.

Внося эту поправку в формулу (14), найдем следующее приближение корня

. (7.15)

Геометрически метод Ньютона (7.15) эквивалентен замене небольшой дуги кривой 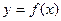касательной, проведенной в некоторой точке касания (Рис. 12).

Рис. 12 Иллюстрация метода Ньютона

Если положить (см. Рис. 12) и, следовательно, то, проведя касательную к кривой 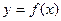в точке , получили бы точку , лежащую вне отрезка , и можем не прийти к корню уравнения (7.1). Поэтому за начальное приближение в формуле (7.15)выбирается тот конец отрезка , для которого знак функции совпадает со знаками второй производной, т. е. .

Теорема. Если , причем отличны от нуля и сохраняют определенные знаки при , удовлетворяющего неравенству , то можно вычислить методом Ньютона по формуле (7.15) единственный корень уравнения (7.1) с любой степенью точности.

Из формулы (7.15) видно, что чем больше численное значение производной в окрестности данного корня, тем меньше поправка, которую нужно прибавить к -му приближению, чтобы получить -ое приближение. Поэтому метод Ньютона особенно удобно применять тогда, когда в окрестности данного корня график функции имеет большую крутизну. Но, если численное значение производной близ корня мало, то поправки будут велики, и вычисление корня по этому методу может оказаться очень долгим, а иногда и вовсе невозможным. Следовательно, если кривая 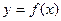вблизи точки пересечения с осью почти горизонтальна, то применять метод Ньютона для решения уравнения (7.1) не рекомендуется.

Для оценки погрешности -го приближения можно воспользоваться формулой

(7.16)

или формулой

, (7.17)

где , .

В общем случае совпадение с точностью до двух последовательных приближений и вовсе не гарантирует, что с той же точностью совпадает значение и корень (Рис. 13).

Рис. 13 О двух последовательных приближениях

Оценки (7.16), (7.17) указывают на квадратичную сходимость метода Ньютона. Поэтому если мало меняется на , то можно пользоваться видоизмененной формулой Ньютона:

(7.18)

В этом случае для получения требуемой точности в отличии от формулы (7.15) необходимо сделать лишь несколько дополнительных шагов.

Не нашли, что искали? Воспользуйтесь поиском: