
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Тема 8. Средние величины и показатели вариации.
В результате изучения этой темы Вы будете
знать:
· сущность средних величин;
· виды средних величин и порядок их исчисления;
· виды показателей вариации и способы их расчета;
уметь:
· рассчитывать средние величины;
· определять показатели вариации;
иметь навыки:
· применять средние величины при обобщении социально-экономических показателей (средняя зарплата, средний возраст, среднесписочная численность и т.д.).
Переходим к одной из наиболее важных тем в курсе статистики - среднимвеличинам и показателям вариации. Что же такое средние и почему эти показатели так важны для анализа статистической информации? Давайте рассмотрим такой пример. Предположим, у банка "Кредит-Банк" (название и приведенные в примере цифры условные) есть несколько филиалов, работающих в разных районах города. В этих филиалах работает разное количество сотрудников, у них разное количество посетителей и т.п. Перед нами как исследователями стоит задача - сравнить эффективность работы филиалов и отдельных сотрудников, чтобы поощрить успешных менеджеров и операционистов и распространить их опыт на другие подразделения, а с теми, кто не слишком хорошо работает, разобраться - в чем причина такой ситуации. Но как это сделать, ведь количество сотрудников и посетителей разное, операции они проводят тоже разные - в одном филиале большое количество посетителей оплачивает, например, коммунальные услуги, в другом больше обслуживается юридических лиц со своими задачами, в третьем - в основном, операции с вкладами граждан и т.п. Чтобы решить эту задачу, мы собирали первичные данные о том, сколько посетителей в день обслуживал каждый операционист в каждом из филиалов в течение месяца, затем сложили эти данные и получили следующую таблицу:
| Филиал | "Центральный" | "Первомайский" | "Заводской" |
| Кол-во клиентов | |||
| Кол-во операционистов |
Какие выводы можно сделать из этой таблицы? Да практически никаких, пока мы только установили некоторый факт – количество клиентов, обслуженных в течение месяца. В «Первомайском» больше всего клиентов, в "Заводском" - меньше, и все. Чтобы продолжить решение нашей задачи и приблизиться к конечной цели - принятию определенного решения, необходимо найти такой показатель, который будет общим для всех филиалов и операционистов, и по которому можно будет сравнить эти группы. Например, показателем эффективности работы операционистов может быть количество клиентов, обслуживаемых ими в день (для простоты условимся, что качество работы всех операционистов примерно одинаково) - чем больше обслужено клиентов, тем лучше работает сотрудник. Но тогда возникает вопрос, как провести такое сравнение - ведь в один день клиентов могло быть много, а в другой - мало, несколько дней у одной из сотрудниц болел ребенок, и она никак не могла сосредоточиться на работе и делала все медленнее, чем обычно, а другой сотрудник неделю был на больничном. И таких случайных факторов в любой работе достаточно много. Как же устранить их влияние и выделить основное, характерное именно для этого сотрудника, или, в общем случае, для изучаемого объекта? Вот здесь-то нам на помощь и приходят средние величины. И в нашем примере сравнить эффективность работы сотрудников банка можно, в частности, по такому показателю, как среднее количество клиентов, обслуживаемых в день. Рассчитать этот показатель очень просто:
1. берем данные о том, сколько клиентов обслуживал конкретный сотрудник каждый день (предположим, в течение месяца);
2. суммируем их, то есть получаем общее количество клиентов, обслуженных данным сотрудником в течение месяца;
3. делим на количество дней, в которые проводилось наблюдение (для каждого сотрудника оно может быть разным).
Полученная цифра и будет средним количеством клиентов, обслуживаемых в день конкретным сотрудником.
В общем виде показатель, который мы рассчитываем, называется " простая средняяарифметическая ", а формула для расчетов выглядит так:
X = 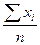
Страшновато смотрится? На самом деле ничего сложного в этой и других статистических формулах нет, просто надо привыкнуть к определенной системе обозначений, принятой в математике и статистике. Если Вы уже знакомы с такими обозначениями, можете двигаться дальше, если же нет - советуем внимательно прочитать комментарий.
Комментарий. В математике и статистике приняты определенные обозначения для различных элементов и действий. Общий объем изучаемой совокупности (количество единиц наблюдения или число вариант и т.п.) обозначается А/ или п. В приведенном выше примере n- это количество дней, в которые проводились измерения количества обслуживаемых клиентов. Каждое конкретное значение (специалисты говорят " варианта") в общем виде обозначается традиционными для переменных величин в математике буквами х, у и т.п. с приписанным справа и чуть ниже обозначением порядкового номера (обычно для этого используются буквы i или j) - получается хi или yj и т.п. В нашем примере х1 - это количество клиентов, обслуженных в первый день наблюдения, х2 - во второй день, х3 - в третий и так далее. Тогда любой ряд данных можно представить в следующем виде – хi. Такой ряд (он называется ряд распределения, но подробно об этом позже) характеризуется еще одной величиной - так называемой частотой (обычно обозначается fi), которая показывает, сколько раз в ряду встречается данная варианта.
∑ (греческая буква, читается "сигма") обозначает сумму всего, что за ней стоит. То есть выражение ∑хi. (дальше мы будем писать просто) означает, что необходимо сложить х1, х2, х3 и так далее до самого последнего хn. А (или другая какая-то буква с чертой над ней) обычно обозначает среднюю величину. Таким образом, формулу простой средней арифметической можно перевести на "человеческий" язык примерно так: "средняя арифметическая равна сумме всех значений икс (в нашем примере это количество обслуженных каждый день клиентов), деленной на количество значений (в нашем примере - дней, в течение которых проводились измерения числа обслуживаемых клиентов)".
Предположим, мы провели измерение количества обслуживаемых клиентов и получили такие данные для операционистов филиала "Заводской":
| Фамилия сотрудника: Алексеева | Всего | ||||||
| Даты | … | 22 (дня, в которые проводилось наблюдение) | |||||
| Количество обслужен -ных клиентов | ….. | 319 (всего обслужено клиентов за все дни наблюдения) |
Данные по другим сотрудникам отдельно приводить не будем, перейдем сразу к сводной таблице.
| Фамилия сотрудника | Общее количество клиентов, обслуженных данным сотрудником за время наблюдения (∑ хi) | Количество дней, в течение которых проводилось наблюдение (n) | Среднее количество клиентов, обслуживаемых в день |
| Алексеева | 319:22 = 14,5 | ||
| Горобец | 328: 18 = 18,2 | ||
| Тимина | 217:25 = 8,7 | ||
| Итого: | 13,3 |
Итак, делим общее количество обслуженных клиентов (864) на общее количество дней, в течение которых проводилось наблюдение (65) и получаем среднее количество клиентов, обслуживаемых в день (округленно 13,3) в филиале "Заводской".
Что нам дает эта цифра? Она важна, в частности, как показатель для сравнения. Например, если в других филиалах этот же показатель значительно выше или ниже, то руководству филиала и банка необходимо задуматься над причинами этого - чем так отличается данный филиал, что в среднем обслуживает намного меньше или больше клиентов. Или можно сравнить средние по нескольким месяцам или кварталам - если этот показатель увеличивается, то, скорее всего, банк успешно развивается, растет профессионализм сотрудников и т.п. Если же среднее количество клиентов становится меньше, то это сигнал о каких-то значительных изменениях, на которые также надо реагировать.
Но вернемся к таблице. Итак, на первый взгляд, мы получили желаемый результат - обобщающий показатель, значение которого практически не зависит ни от количества дней, в течение которых проводилось наблюдение, ни от случайностей типа болезни, плохого настроения и т.п. Из последнего столбца таблицы видно, что в среднем больше всего клиентов в день обслуживает Горобец, а у Тиминой этот показатель в два с лишним раза меньше, следовательно... Но не спешите с выводами! Помните, еще в самом начале этой тетради мы говорили о том, что правильные выводы можно делать только из достоверной и полной информации. Так вот, вывод о том, что Тимина работает значительно менее эффективно, чем другие сотрудники, можно сделать, только если они находятся в равных условиях - обслуживают один тип клиентов, проводят одни и те же операции и т.п. А если она занимается, например, обслуживанием юридических лиц или решением особо сложных вопросов, требующих значительных затрат времени?
Но конечной целью нашего анализа является сравнение всех трех филиалов. Одним из возможных показателей для сравнения может быть среднее количество клиентов, обслуживаемых одним операционистом в месяц, так как оно определяется и работой операционистов, и общей организацией труда в филиале, и другими факторами.
Считаем:
| Филиал | "Центральный" | "Первомайский" | "Заводской" |
| Кол-во клиентов | |||
| Кол-во операционистов | |||
| Среднее кол-во клиентов обслуживаемое одним операционистом | 1620:7= 231, 4 | ||
ЗАДАНИЕ 5.
Среднее количество клиентов, обслуживаемое одним операционистом, для филиалов "Первомайский" и "Заводской" рассчитайте, пожалуйста, сами и впишите результат в таблицу.
Если все филиалы выполняют одни и те же операции и находятся в примерно равных условиях, то получается, что в "Первомайском" работа, в том числе по привлечению клиентов, организована значительно эффективнее. Разумеется, это только учебный пример, и в реальной жизни вряд ли можно встретить такие значительные различия в эффективности работы похожих организаций. Тем более не стоит делать выводы об эффективности только по одному показателю, на самом деле необходимо учитывать большое количество различных факторов, влияющих на эффективность работы организации.
Приведенную выше формулу простой средней арифметической можно применять не всегда, а только тогда, когда значения не повторяются или их частоты (сколько раз это значение встречается в ряду) равны. Если же, например, у нас в результате наблюдения получился такой ряд, в котором некоторые значения встречаются несколько раз (повторяются):
| Даты | Всего | ||||||||||
| Количество обслуженных клиентов | .11 |
то более точную характеристику ряда дает средняя арифметическая взвешенная, которая рассчитывается по следующей формуле:
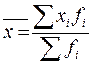
где хi - значения (сколько клиентов было обслужено),
fi - веса (частоты - сколько раз это значение встречается в ряду).
Тогда наш расчет будет выглядеть так:
| Хвз |
= 13*2 + 11*3 + 16*2 + 18*3 = 145 = 14,5
2 + 3 + 2 + 3 10
Средняя величина признака - это отношение определенных показателей, поэтому прежде чем рассчитывать какие-либо средние, необходимо выяснить и обосновать, какие именно показатели использовать для расчетов. Для этого применяется так называемая логическая формула средней, которая записывается словами. В общем виде логическую формулу средней можно определить так:
| средняя величина признака= |
общий объем изучаемого призна ка количество объектов совокупности, обладающих данным признаком
Например, для средней заработной платы логическая формула средней будет выглядеть как
средняя заработная плата
в расчете на одного сотрудника = общий фонд заработной платы
количество сотрудников
Существуют и другие виды средних величин, у каждого из которых есть своя специфика.
Мы рассмотрим еще так называемые структурные средние - моду и медиану.
Мода - это наиболее часто встречающееся в ряду значение.
Например, представим такой ряд оценок:
В этом ряду значение моды - 4, так как именно эта оценка встречается чаще всего. Бывают случаи, когда характеристику ряда удобнее давать не по средней арифметической, а по моде, так как она более точно описывает основное свойство ряда, особенно, если в ряду есть несколько сильно отклоняющихся от среднего значений.
Ниже, в таблице представлены виды и расчет наиболее часто используемых средних величин.
Не нашли, что искали? Воспользуйтесь поиском: