ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Простая средняя арифметическая для интервального ряда
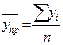
где уi - уровни ряда от 1 до n, n -число уровней ряда.
Пример. Для наших данных о количестве посетителей магазина "Заводской" можно рассчитать простую среднюю арифметическую, так как интервалы равные (1 неделя). Для этого суммируем количество посетителей за 8 недель (138 + 234+288 + +343+388+446+491+532=2860), делим полученную сумму на 8 (так как у нас всего 8 уровней ряда) и получаем результат — среднее количество посетителей в неделю — 357,5.
Средняя арифметическая взвешенная для интервального ряда с неравными интервалами:
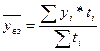
где уi - уровни ряда,
ti - веса (в данном случае количество интервалов времени - дней, недель, месяцев и т.п. - между смежными датами).
Пример. Предположим, что в некоторой фирме с 1 по 15 число месяца работали 12 человек, с 16 по 25 - 18 человек, а с 26 по 30 - 21 человек.
Задача - рассчитать такой часто применяющийся показатель, как среднесписочное число работников за месяц. Запишем интервальный ряд:
| Дата (t) | 1 – 15 | 16 – 25 | 26 - 30 |
| Кол-во работников (y) |
Интервалы неравные, поэтому считаем по формуле средней арифметической взвешенной для интервального ряда
12 (чел) * 15(дней) + 18*10 + 24*5 = 480 = 16
30 (дней) 30
Результат - среднесписочное число работников за месяц -16 (чел.).
Для моментных рядов используются другие формулы. Средний уровень моментного ряда с равными промежутками между датами определяется по формуле средней хронологической для моментного ряда:
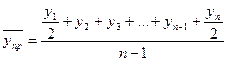
где п -число дат,
у1..., уn - уровни ряда в соответствующие моменты времени.
Пример. Предположим, нам нужно посчитать средний месячный курс доллара в квартале, и мы имеем данные о курсе доллара на первое число каждого месяца (цифры условные). Моментный ряд в этом случае выглядит так:
| Дата | 01.04 | 01.05 | 01.06 | 01.07 |
| Курс $ (руб) | 24,26 | 25,10 | 25,24 | 25,86 |
Проводим расчет:
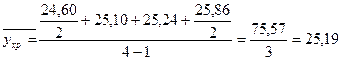
Следовательно, средний курс за квартал равен 25,19(руб./$).
Средний уровень моментных рядов с неравномерными промежутками междудатами рассчитывается по формуле средней хронологической взвешенной:
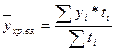
где у1 - уровни ряда,
t1 - количество дней (недель, месяцев и т.п.) между смежными датами.
Пример. Предположим, на 1 января отчетного года стоимость основных фондов предприятия составила 75 млн. руб. В марте были приобретены основные фонды на сумму 2 млн. руб., в мае выбыло основных фондов на 7 млн. руб., а в сентябре - еще приобретено основных фондов на 8 млн. руб. Необходимо рассчитать среднегодовую стоимость основных фондов предприятия. Промежутки между датами неравные, поэтому используем формулу средней хронологической взвешенной. Для наглядности расчетов составляем таблицу:
| Даты | Стоимость основных фондов (млн. руб.) | Количество месяцев между смежными датами (число месяцев, в течение которых стоимость фондов не изменялась) | У,*, |
| 1 января | 3 (с января по март включительно) | 225(75x3) | |
| 1 апреля | 77(75+2) | 2 (апрель и май) | 154(77x2) |
| 1 июня | 70(77-7) | 4 (с июня по сентябрь включительно) | 280(70x4) |
| 1 октября | 78(70+8) | 3 (с октября по декабрь включительно) | 234(78x3) |
| Итого: | 12(∑t1, то есть всего месяцев) | (∑yiti) |
Делим в соответствии с формулой 893 на 12 и получаем среднегодовую стоимость основных фондов - 74,417 млн. руб.
Вы можете спросить, зачем такие сложности, ведь можно было посчитать по формуле обычной средней арифметической - сложить стоимость на начало и на конец года и разделить на два. О том, что в таких случаях лучше применять среднюю взвешенную, мы уже говорили в Теме 8, но давайте проверим, что получится - (75+78)/2=76,5 млн. руб. А рассчитанный по средней взвешенной - 74,417 млн. руб. Разница практически в 2 миллиона рублей, и только из-за методики расчета! А ведь со стоимости основных фондов платятся налоги. Представляете, сколько можно сэкономить, если хорошо знать статистику и правильно применять соответствующие формулы.
ЗАДАНИЕ 11.
В течение полугода Вам приходилось несколько раз изменять цену на свой товар. Для сравнения своей цены с ценами конкурентов Вам необходимо рассчитать, пользуясь приведенными ниже данными, среднюю цену на товар за это полугодие:
| Дата | 1 января | 1 марта | 1 мая | 1 июля |
| Цена товара |
Завершая эту тему, стоит сказать и о том, что для получения логичных правильных результатов и выводов при построении и анализе рядов динамики, статистические данные должны быть - по территории, единицам измерения, времени регистрации, ценам и т.п. Например, если Вы в одном месяце будете регистрировать количество посетителей магазина только вечером, в другом - только утром, а затем попытаетесь сравнить получившиеся ряды динамики, формально Вы получите какие-то данные, но в них будет мало смысла, и на их основе нельзя будет сделать никаких практических выводов. Или, если Вы хотите сравнить динамику объема продаж (в рублях) Вашей компании за этот год и позапрошлый, для действительно адекватных выводов Вам придется сначала привести все данные к так называемым сопоставимым ценам, то есть ценам одного определенного (базисного) периода и одинаково описывающим стоимость товара, чтобы не получилось, что Вы сравниваете тысячи с миллионами, а доллары – с рублями.
Подведем итоги
- Статистический ряд распределения представляет собой упорядоченное распределение единиц изучаемой совокупности по определенному варьирующему (изменяющемуся) признаку.
- Ряды распределения бывают атрибутивные (построенные по качественному признаку) и вариационные (построенные по количественному признаку).
- Вариационные ряды распределения состоят из двух элементов - вариант (значений) и частот (весов).
- Вариационные ряды делятся на дискретные и непрерывные.
- Если признак изменяется непрерывно или количество значений дискретного признака достаточно велико, строят интервальные ряды.
- Для изучения изменений объекта во времени строят и анализируют ряды динамики.
- Для анализа динамических рядов разработана система показателей динамики, в которую входят: абсолютный прирост (сокращение), темп и коэффициент роста, темп прироста, абсолютное значение одного процента прироста.
- Все показатели динамики могут рассчитываться на постоянной (базисный способ) и переменной (цепной способ) базе.
- Для получения логичных правильных результатов и выводов при построении и анализе рядов распределения и динамики статистические данные должны быть сопоставимы.
Тема 11. Индексы.
В результате изучения этой темы Вы будете
знать:
· что такое индексы и для чего они применяются;
· виды индексов, порядок их исчисления и взаимосвязи;
уметь:
· рассчитывать индивидуальные и общие индексы (цен, стоимости, физического объема);
иметь навыки:
· применять индексный метод при анализе социально-экономических показателей.
Наряду со средними и показателями вариации одними из наиболее часто применяемых в статистике показателей являются индексы (от латинского слова index - "указатель, показатель").
С их помощью можно:
· характеризовать развитие экономики в целом и отдельных отраслей;
· анализировать результаты деятельности предприятий и организаций;
· исследовать роль отдельных факторов в формировании социально-экономических показателей.
Индексы также широко используются при международных сопоставлениях экономических показателей, определении уровня жизни, мониторинге деловой активности и т.д.
В статистике под индексом понимают относительный показатель, характеризующий изменение величины какого-либо объекта во времени, пространстве или по сравнению с эталоном (нормативом, планом, прогнозом и т.п.).
Например, предприятия обычно выпускают много разных видов продукции и продают их по разным ценам, поэтому нельзя простым сложением количества всех видов продукции в натуральных единицах измерения (штуках, тоннах, метрах и т.п.) получить общую характеристику объема производства. Представьте, что будет, если мы начнем складывать друг с другом метры ткани, килограммы кожи и штуки костюмов и платьев, и на основании таких несуразных чисел делать выводы об объеме производства предприятия. Вот тут-то и приходят на помощь индексы, которые позволяют привести разнородные продукты к соизмеримым величинам (мерам соизмерения). В качестве меры соизмерения разнородных продуктов можно использовать цену, себестоимость или трудоемкость единицы продукции.
Для удобства восприятия индексов в теории статистики разработаны и приняты определенные обозначения. Каждая индексируемая величина имеет свое обозначение:
qi - обозначается количество единиц данного вида продукции;
pi - цену единицы продукции;
уi - себестоимость единицы продукции;
ti -трудоемкость (затраты времени на производство) единицы продукции, и так далее.
Чтобы различать, к какому периоду относятся индексы, их также обозначают и цифрами - 0 для базисного периода (вспомните, какой период называется базисным, а какой -отчетным, мы это изучали в предыдущей теме), 1 - для отчетного (сравниваемого).
Различают индивидуальные индексы, которые характеризуют изменение только одного элемента совокупности, например, выпуск одного вида продукции, и общие (сводные) индексы, характеризующие всю совокупность или сложное явление. Индивидуальные индексы обозначаются i, общие - I, при этом для всех типов индексов внизу справа добавляется обозначение индексируемого показателя. Например, ip - индивидуальный индекс цен, Iq - общий индекс объема продукции. Индексы также бывают базисные (рассчитанные базисным способом, о котором мы говорили в предыдущей теме), и цепные (рассчитанные цепным способом). Общие индексы могут быть также построены двумя способами – как агрегатные, и как средние из индивидуальных. Примеры и способы расчета основных типов индексов мы с Вами сейчас рассмотрим.
Индивидуальные индексы рассчитываются достаточно просто - они представляют собой отношение двух индексируемых величин:
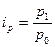- индивидуальный индекс цен,
где р1 - цена единицы продукции в отчетный период,
р0 -цена единицы той же продукции в базисный период.
Если в прошлом (базисном) году производимый швейной фабрикой костюм стоил, предположим, 600 рублей, а в этом (отчетном) - 720 рублей, то индекс цен на данный товар составит 1,2 (720 делим на 600 и получаем 1,2). Это означает, что цена на костюм в отчетном периоде увеличилась в 1,2 раза по сравнению с базисным периодом. Так же считаются и другие индивидуальные индексы.
Если же мы хотим выяснить, например, как изменилась общая стоимость произведенной швейной фабрикой продукции по сравнению с прошлым годом, то необходимо рассчитать общий индекс стоимости по следующей формуле:
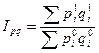
То есть мы отдельно для отчетного и базисного периодов умножаем количество произведенной продукции каждого вида на стоимость этого вида продукции, полученные цифры складываем и получаем общую стоимость продукции за соответствующий период (например, 1000 рубашек по 25 рублей + 400 костюмов по 720 рублей + 600 платьев по 500 рублей составит общую стоимость продукции за отчетный период - 613 тыс. руб., а 800 рубашек по 25 рублей + 400 костюмов по 600 рублей + 500 платьев по 400 рублей составит общую стоимость продукции за базисный период - 460 тыс. руб.). Затем делим стоимость за отчетный период на стоимость за базовый период (613 делим на 460) и получаем общий индекс стоимости продукции - приблизительно 1,33.
С одной стороны, мы получили то, что хотели - сравнили стоимость продукции фабрики за отчетный и базисный период. С другой стороны, у способа, которым мы рассчитывали индекс, есть существенный недостаток: имея только такой индекс, нельзя сказать, за счет чего именно увеличилась стоимость продукции - за счет увеличения физического объема производства (в штуках, метрах и т.п.), повышения цены на продукцию, или и того и другого вместе. Почему так происходит? Потому что в данной формуле одновременно изменяются обе величины - и в числителе, и в знаменателе, в данном случае и цена, и объем производства. Этот недостаток устраняется при помощи агрегатных индексов, основной особенностью которых является то, что в числителе и знаменателе меняется только одна величина, значение же другой (соизмеримой), остается неизменным.
Например, если в формуле общего индекса стоимости устранить влияние изменения цен, рассчитав и числитель, и знаменатель в ценах базисного периода, то получим так называемый агрегатный индекс физического объема:
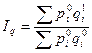
Этот индекс, предложенный немецким экономистом Э. Ласпейресом, показывает, во сколько раз изменился физический объем продукции в отчетном периоде по сравнению с базисным. Таким же образом можно рассчитывать агрегатные индексы цен, себестоимости, трудоемкости и т.п.
Агрегатный способ вычисления индексов в статистике является наиболее распространенным, но не единственным. В тех случаях, когда имеющейся информации недостаточно для расчета агрегатных индексов, используют способ расчета средних из индивидуальных индексов. Например, когда неизвестны количества произведенных отдельных видов продукции, но известны индивидуальные индексы для этих видов продукции (i) и стоимость каждого вида продукции базисного периода (р10q10, можно легко определить средний арифметический индекс физического объема продукции по формуле:
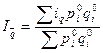
Если же известны данные, которые позволяют вычислить только числитель агрегатного индекса физического объема, то, выразив продукцию базисного периода как q10 = q11 / pq можно заменить знаменатель в формуле агрегатного индекса физического объема, и получить формулу среднего гармонического индекса физического объема:
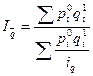
Как мы уже говорили, индексы применяют для анализа сложных экономических явлений, в частности для описания изменений цен на потребительском уровне в городах, регионах и стране в целом. Для этого рассчитывают так называемый индекс потребительских цен:
стоимость рыночной корзины базисного периода в текущем году *100
ИПЦ = стоимость рыночной корзины базисного года в базисном году
Этот индекс характеризует изменение во времени общего уровня цен на товары и услуги, приобретаемые населением для непроизводственного потребления. Он является одним из важнейших показателей инфляции и используется для анализа социально-экономических процессов, регулирования курса национальной валюты, определения уровня минимальных социальных гарантий и других целей.
Индексный метод широко используется и в аналитических целях, так как дает возможность устранить влияние отдельных факторов, характеризующих явление, и ответить на вопрос, за счет изменения каких составляющих изменяется объект в целом.
Ниже, в таблице представлены виды и расчет наиболее распространенных экономических индексов.
Не нашли, что искали? Воспользуйтесь поиском: