
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Тема 9. Статистическое изучение связей между явлениями.
В результате изучения этой темы Вы будете
иметь представление:
· о том, что такое функциональные и стохастические связи;
· о методах установления зависимостей между признаками.
Одна из основных задач статистики - изучение закономерностей, то есть устойчивых связей между различными явлениями и процессами. Помните, когда мы с Вами говорили об аналитической группировке, из приведенных в примере данных можно было сделать предварительный вывод о том, в каком издании эффективнее размещать рекламу различных товаров. Тогда мы упоминали понятие связи - конкретно в примере речь шла о связи между тематикой издания и видом товара, рекламу которого в этом издании лучше размещать. Многие социально-экономические процессы и явления, изучением которых занимается статистика, связаны между собой, то есть оказывают влияние друг на друга. Например, инфляция связана с объемом эмиссии (выпускаемых Центральным Банком в обращение денег), заработная плата сотрудников предприятия зависит, в частности, от объема произведенной и проданной продукции и т.п. Наличие связи между одними явлениями можно легко установить "на уровне здравого смысла, то есть не пользуясь никакими специальными средствами и методами. Например, достаточно очевидно, что летом объем продажи мороженого выше, чем зимой, следовательно, объем продажи мороженого связан с сезоном. Связи же между многими социально-экономическими явлениями далеко не так очевидны, и поэтому для их изучения в статистике разработаны специальные методы. Наиболее распространенные и часто использующиеся - это регрессионный и корреляционный анализ. Но, прежде чем мы перейдем к знакомству с этими методами, поговорим немного о различных типах связей.
Вы, наверное, помните, что в математике есть такое понятие функция, которое в общем виде выражается так:
y = f (x)
Это означает, что значения у строго определенным образом зависят от значений х, а вид этой зависимости может быть различным. Например, при формуле у=5х каждому значению х соответствует в 5 раз большее значение у. Такую связь называют функциональной, основное ее свойство в том, что каждому значению независимого признака х соответствует строго определенное значение зависимого признака у. Такой вид связи характерен в основном для явлений, которые изучаются точными науками - математикой, физикой и т.п. В реальной общественной жизни такой вид связи встречается очень редко, например, это может быть связь между объемом выполненной работы и оплатой при простой сдельной системе оплаты труда - если за печать одной страницы текста машинистке платят 2 рубля, то легко можно посчитать по уравнению у=2х, сколько она получит за 5, 20 или 163 страницы соответственно, 10, 40 или 326 рублей. Но в основном социально-экономические явления связаны с большим количеством различных факторов, точно определить влияние которых практически невозможно. Поэтому всегда сохраняется некоторая неопределенность, которая характеризуется вероятностью наступления того или иного события. Например, при приеме на работу в фирму нескольких новых агентов по продаже товара общий объем продажи товара, скорее всего, изменится, но на сколько именно - точно сказать невозможно, так как это зависит от многих факторов (опыта работы агентов с данным товаром, экономической ситуации в тех районах, где они будут работать, личных качеств агентов и т.п.). В таких случаях мы можем только определить, что с большой вероятностью объем продаж в следующем месяце будет находиться в некоторых пределах - скажем, от 120 до 150 штук. Такой тип связи, когда значение зависимой переменной у' может быть предсказано на основе имеющихся значений х с некоторой вероятностью, называется стохастической, и именно стохастическая (вероятностная) связь характерна для социально-экономических явлений и процессов. У стохастической связи есть очень важная особенность - она обнаруживается не на уровне единичных случаев, а в массовых явлениях, и чем больше у нас результатов наблюдений, тем точнее мы можем описать связь между изучаемыми явлениями. Например, если мы, приняв на работу одного-двух новых агентов по продаже и не увидев изменения количества проданного товара за месяц, попытаемся сделать вывод о том, что прием новых агентов практически не влияет на объем продаж, то, скорее всего, мы будем не правы, так как эти конкретные агенты, не продавшие за месяц ничего, могли оказаться просто неопытными, или работали не с теми потенциальными потребителями и не в том районе, в котором следовало, и т.п. То есть из единичного случая нельзя делать вывод о том, есть связь между количеством агентов и объемом продаж или нет. Вот если количество агентов увеличилось на 50 человек, а объем продаж практически не изменился, тогда уже отсутствие связи более очевидно, и есть смысл задуматься над причинами такого положения дел - или агенты неподготовленные, или товар не нужен на рынке, или что-то еще. Еще раз обращаем Ваше внимание - статистика изучает массовыеявления, и только на основании достаточной информации можно делать серьезные выводы.
Еще стоит вспомнить о том, что связь бывает прямая и обратная. Прямой называется такая связь, при которой с увеличением одного признака увеличивается и другой.
Например, чем больше количество страниц, которое машинистка может напечатать в час, тем больше документов она напечатает за рабочий день. При обратной связи все наоборот - с увеличением одного признака другой уменьшается, или при уменьшении одного другой увеличивается. Например, чем меньше времени тратит машинистка на печать одной страницы, тем больше страниц она напечатает в день, тем выше, соответственно, ее производительность труда (объем работы, выполняемый в единицу времени).
Итак, Вы познакомились со стохастической связью. Частные случаи этого типа связи, которые мы и будем рассматривать - это корреляционная и регрессионная. Какими же методами изучаются эти связи? Начнем с самых простых.
Метод аналитических группировок. С этим методом Вы уже немного знакомы (вспомните пример с размещением рекламы, который мы рассматривали, когда изучали группировки) - группируя имеющиеся данные по определенным признакам, можно оценить, существует между признаками какая-либо связь или нет, и при необходимости изучить этот вопрос более глубоко.
Метод сопоставления параллельных рядов. Суть этого метода в том, что имеющиеся данные выписывают в два ряда значения независимого (факторного) признака - в один, а зависимого (результативного) - в другой, и, сопоставляя эти ряды, отслеживают, как изменяется зависимый признак. Рассмотрим пример с анализом связи между количеством агентов и объемом продаж товара. Предположим, мы изучили финансовые документы и получили следующие данные:
| Кол-во агентов | ||||||
| Объем продаж товара (штук) |
Даже "невооруженным глазом" можно заметить, что чем больше агентов, тем больше единиц товара продается, следовательно, между признаками "количество агентов" и "объем продаж" есть связь.
ЗАДАНИЕ 7.
Если эти данные представить графически, то наличие связи будет еще более наглядно - попробуйте самостоятельно построить график зависимости объемов продаж от количества агентов и объясните, по каким признакам Вы можете сделать вывод о том, что связь есть.
Метод, которым Вы только что воспользовались, называется графическим методом изучения связи между признаками. Им также пользуются для определения наличия и вида связи. Для этого на графике располагают точки, соответствующие полученным данным, и по виду расположения точек делают предварительные выводы о связи.
А если бы объем продаж практически не изменялся, вывод был бы другим - связи между этими признаками, скорее всего, нет. Почему "скорее всего"? Да потому, что имеющейся у нас информации недостаточно, чтобы сказать об этом точно - может быть, мы неправильно собирали данные, или не учли сезонный спад спроса на товар - мало ли причин, по которым товар не продается. Так что вывод о том, что количество агентов надо сокращать, делать пока рановато.
Пользуясь описанными выше методами, можно в принципе установить, есть связь между какими-то признаками или нет.
Но очень часто необходимо не только знать о том, что между определенными признаками связь есть, но и определять, насколько она тесная, и как изменение одного признака будет влиять на изменение другого. Например, рост цен на бензин ведет к увеличению цен на большинство товаров и услуг. Но одни товары, в себестоимости которых транспортные расходы невелики, подорожают совсем немного, а другие, цена которых сильно зависит от стоимости доставки, могут подорожать весьма значительно. Как узнать, насколько изменяется цена товаров в зависимости от цены на топливо? Для решения такого типа задач и существует регрессионный анализ, позволяющий установить вид связи между признаками (линейная или нелинейная, прямая или обратная) и определить расчетные значения зависимой переменной. Мы с Вами рассмотрим в качестве примера уравнение однофакторной (парной) линейной регрессии, которое имеет следующий вид:
 =
= 
где у - теоретические значения результативного признака, полученные по уравнению регрессии, а0 и а] - коэффициенты (параметры) уравнения регрессии.
"Физический" смысл этого уравнения в следующем:
· все уравнение в целом показывает, как признак у изменяется в зависимости от изменения признака х;
· коэффициент а1 говорит о силе связи между признаками х и у, то есть, чем он больше, тем больше изменяется у при изменении х на одну единицу (сравните, например уравнения у=2х и у=7х), а его знак - о направлении связи, если а1 положительный, то связь прямая, а если отрицательный - обратная.
Параметры уравнения регрессии обычно находят методом наименьших квадратов (он реализован в различных математических и статистических компьютерных программах, регрессионный анализ можно также проводить при помощи электронных таблиц Ехсе1), но это связано с решением достаточно сложных систем уравнений, поэтому иногда их вычисляют по следующим формулам:


Пример (из книги "Теория статистики", В.М.Гусаров, М.,"Аудит", 1998). Рассмотрим построение однофакторного уравнения регрессии зависимости производительности труда у от стажа работы х по данным таблицы (10 рабочих одной бригады заняты производством радиоэлектронных изделий, данные ранжированы по стажу их работы).
Исходя из экономических соображений, стаж работы выбран в качестве независимой переменной х. Сопоставление данных параллельных рядов признаков х и у (см. табл.) показывает, что с возрастанием признака х (стаж работы), растет, хотя и не всегда, результативный признак у (производительность труда). Следовательно, между х и у существует прямая зависимость, пусть неполная, но выраженная достаточно ясно.
Распределение рабочих бригады по выработке и стажу работы.
| Исходные данные | Расчетные значения | |||||
| Номер рабочего | Стаж работы, годы (х) | Дневная выработка рабочего, шт. (У) | х2 | у2 | ху | у |
| 4,6 | ||||||
| 5,2 | ||||||
| 5,8 | ||||||
| 6,4 | ||||||
| 7,0 | ||||||
| 7,6 | ||||||
| 8,2 | ||||||
| 8,8 | ||||||
| 9,4 | ||||||
| 10,0 | ||||||
| Итого | ∑х=55 | ∑у=73 | ∑х2=385 | ∑у2=565 | ∑ху=451 | 73,0 |
ЗАДАНИЕ 8
Для уточнения формы связи между рассматриваемыми признаками можно использовать графический метод. Постройте самостоятельно график зависимости выработки от стажа работы по приведенной в примере таблице (нанесите на график соответствующие точки и соедините их отрезками).
Дневная выработка, шт

 Стаж работы, годы (х)
Стаж работы, годы (х)
Анализируя ломаную линию, можно предположить, что возрастание выработки (у) идет равномерно, пропорционально росту стажа работы (х). В основе этой зависимости в данных конкретных условиях лежит прямолинейная связь, которая может быть выражена линейным уравнением регрессии:
у = а0 + а1 х
где у -теоретические значения результативного признака (выработки одного рабочего, шт.), полученные по уравнению регрессии,
а0 и а1 -неизвестные параметры уравнения регрессии,
х - стаж работы рабочих, годы.
Пользуясь расчетными значениями (см. табл.), вычисляем параметры для данного уравнения регрессии.
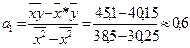

Следовательно, регрессионная модель распределения выработки по стажу работы для данного примера может быть записана в виде конкретного простого уравнения регрессии:

Это уравнение характеризует зависимость среднего уровня выработки рабочими бригады от стажа работы.
Экономически параметры регрессии можно интерпретировать так:
• параметр а1>0, следовательно, связь прямая, то есть с увеличением стажа выработка также увеличивается;
• величина этого параметра (0,6) свидетельствует о том, что при возрастании стажа на 1 год дневная выработка рабочего увеличивается в среднем на 0,6 изделия.
Для удобства интерпретации параметра а] используют так называемый коэффициент эластичности (с понятием эластичности вы подробно познакомитесь в Рабочих тетрадях по экономике и маркетингу). Он показывает средние изменения результативного признака при изменении факторного признака на 1% и вычисляется по следующей формуле (%):

В рассмотренном примере Э = 0,6 * 
Это означает, что с возрастанием стажа работы на 1% можно ожидать роста производительности труда в среднем на 0,45%.
Для измерения тесноты связи, то есть насколько сильно связаны друг с другом изучаемые признаки, пользуются таким показателем, как коэффициент корреляции. Он рассчитывается на основе вычисления средних и средних квадратических отклонений (о которых мы говорили в предыдущей теме) признаков по следующим формулам:

Это линейный коэффициент корреляции для двух признаков –х и у. Коэффициент корреляции изменяется от -1 до 1. Положительные значения коэффициента корреляции говорят о прямой связи, отрицательные - об обратной. Чем ближе значение коэффициента корреляции к 1 (или -1), тем сильнее связь между изучаемыми признаками, соответственно, чем ближе к 0, тем меньше теснота связи. При уровне корреляции приблизительно 0,6-0,7 по модулю уже можно говорить о наличии связи.
Например, коэффициент корреляции между стажем рабочих и выработкой (из рассмотренного нами выше примера) равен 0,96 – это значит, что между стажем работы и выработкой существует прямая и достаточно сильная связь. В нашем примере с зависимостью объема продаж от количества агентов также можно при помощи коэффициента корреляции обнаружить устойчивую прямую связь - коэффициент корреляции равен 0,99. Кроме линейного существуют и другие виды коэффициентов корреляции.. Расчет коэффициента корреляции также возможен в электронных таблицах Ехсе1 и специальных статистических пакетах программ.
Но при всем богатстве возможностей анализа данных и поиска связей между признаками и явлениями, прежде чем выявлять и анализировать какие-то связи, следует максимально подробно и логично описать самому себе, почему Вы предполагаете, что между данными признаками может быть связь, по каким основаниям можно сделать вывод о том, что она есть и как это можно проверить. То есть Вам нужно составить небольшой план анализа полученных данных. Это поможет избежать ошибок как в самом анализе, так и в выводах, которые Вы будете делать на его основе. И еще одно очень важное замечание - корреляционная связь совершенно не обязательно является причинно-следственной, если два явления связаны друг с другом, то это еще не значит, что одно является причиной другого, они просто изменяются сходным образом, возможно под воздействием совсем других факторов. Можно привести такой пример - очевидно, что летом увеличивается объем продаж темных очков и мороженого. Вероятно, между объемами продаж мороженого и темных очков существует достаточно тесная связь с высоким коэффициентом корреляции. Но из этого не следует и не может следовать, что люди едят больше мороженого потому, что покупают темные очки, или покупают темные очки потому, что едят мороженое. Рост объемов продаж обоих товаров связан с третьим фактором - сезоном, который и определяет во многом такую связь. Так что воздержитесь от поспешных выводов, если хотите, чтобы Ваши решения и действия приводили к положительным результатам.
Подведем итоги
Не нашли, что искали? Воспользуйтесь поиском: