ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ВИДЫ И РАСЧЕТ СРЕДНИХ ВЕЛИЧИН
| Методика расчета в области применения средней | Пример | ||||||||||||||||||||||||||||||||||||||||||||||||
| 1.Простая средняя арифметическая величина X1=∑Xi/n, где Х1 – среднее значение величины, ∑Хi – сумма значений осредняемого признака, n – число показаний Используется в тех случаях, когда расчет осуществляется по не сгруппированным данным | В бригаде из 7 человек зафиксирован следующий стаж работы по специальности: 10,3,5,12,11,7,9 лет. Определить средний стаж работы Х1 = ∑Хi/n= (10+305+12+11+7+9)/7=8,1 года – средний стаж рабочих бригады | ||||||||||||||||||||||||||||||||||||||||||||||||
| 2. Средняя арифметическая взвешенная Х2=∑Xifi/∑fi, где fi – частота признака Применяется в тех случаях, когда отдельное значение осредняемого признака повторяется несколько раз | Продажи акций АО «Русский хлеб» на торгах фондовой биржи
Определить средний курс продаж акций на торгах. Х2=∑Xifi/∑fi = (500*1080+300*1090+1100*1145)/(500+300 +1100) = 1112,9 руб. – средний курс продажи акций на торгах | ||||||||||||||||||||||||||||||||||||||||||||||||
| 3. Средняя гармоническая – X3=∑Wi/ ∑(Wi /Xi), где Wi- значение варианты, Wi /Xi – обращенная варианта Это превращенная форма средней арифметической величины. Вместо гармонической средней всегда можно рассчитать среднюю арифметическую, сделав предварительные расчеты. Существует гармо-ническая взвешенная и не взвешенная | Валовый сбор и урожайность подсолничнека по центрально-черноземному району (в хозяйствах всех категорий)
Определить среднюю урожайность подсолнечника. X3=(970+2040+5+160+690)/(970/16,1+2040/9,5+5/4,8+160/10,9 +690/7)=9,9 ц/га – средняя урожайность подсолничнека | ||||||||||||||||||||||||||||||||||||||||||||||||
| 4. Структурные средние: 4.1. Мода (Мо)–применяется для характеристики. Мода – чаще всего встречающийся вариант (типичное значение). Ряд значений, для которого определяется мода, называется модальным. В дискретном ряду мода – это варианта с наибольшей частотой. Если варианта в ряду представлена интервалом значений, то берется середина интервала (средняя из крайних значений интервала. 4.2. Медиана (Ме) – средняя варианта упоря-доченного (ранжирован-ного) вариационного ряда. Если вариационный ряд имеет четное число членов, то медиана (Ме) рассчтыва-ется как полу сумма двух средних вариант. Для интервального ряда медиана рассчитывается более сложно по специаль-ным формулам. | 4.1. Мода
Наибольшим спросом пользуется размер обуви 36 – это и есть среднее (типичное) значение ряда. Средний стаж работников 7 лет = (6+8)/2 – середина интервала.
4.2. Семь членов бригады имеют следующий стаж работы:
Определить средний стаж рабочмх. Ранжируем ряд: 3 5 7 9 10 11 12 Ме Средний стаж рабочих приблизительно 9 лет (см. расчет простой средней арифметической величины по этим же данным). |
ЗАДАНИЕ 6
В течение двух недель в кинотеатре подсчитывали количество зрителей и получили следующие данные:
| День недели | Утренние и дневные сеансы | Вечерние сеансы |
| 1-я неделя | ||
| Понедельник | ||
| Вторник | ||
| Среда | ||
| Четверг | ||
| Пятница | ||
| Суббота | ||
| Воскресенье | ||
| 2-я неделя | ||
| Понедельник | ||
| Вторник | ||
| Среда | ||
| Четверг | ||
| Пятница | ||
| Суббота | ||
| Воскресенье |
По приведенным в таблице данным рассчитайте следующие показатели:
- среднее количество зрителей в день
- среднее количество зрителей в неделю
- среднее количество зрителей в будние дни
- среднее количество зрителей в выходные дни
- среднее количество зрителей на утренних и дневных сеансах
- среднее количество зрителей на вечерних сеансах
- среднее количество зрителей в первую неделю
- среднее количество зрителей во вторую неделю
Другая структурная средняя характеристика - медиана - это значение, стоящее в центре ранжированного (упорядоченного по возрастанию или убыванию) ряда. Она как бы делит ряд на две равных части - со значениями больше медианы и меньше ее. Например, для следующего ряда показателей заработной платы 9 сотрудников организации:
630 650 680 690 700 710 720 730 750
медиана равна 700, так как именно эта варианта стоит в середине ряда. В данном случае медиана означает, что половина сотрудников получала заработную плату менее 700 рублей, а половина - более 700. Если ряд состоит из четного количества вариант, то медиана вычисляется как средняя арифметическая из двух стоящих в центре ряда вариант.
До сих пор речь шла только о средних характеристиках какой-либо совокупности. Но одни только средние не всегда могут полно охарактеризовать совокупность. Сравните, например, два следующих ряда зарплат, получаемых двумя сотрудниками в течение полугода:
700 710 700 700 690 700
500 700 900 700 600 800
Если Вы посчитаете средние месячные зарплаты сотрудников, то увидите, что они одинаковые - 700. Однако Вы видите, что ряды сильно отличаются - во втором ряду значительно больше вариация (разброс), то есть отклонение значений друг от друга и, соответственно, от среднего. Чтобы более полно и точно описывать совокупности, кроме средних в статистике применяют еще и показатели вариации, которые как раз и описывают разброс значений совокупности.
Основные показатели вариации - это размах вариации, дисперсия и коэффициент вариации.
Размах вариации - это разность между максимальным и минимальным значениями совокупности. В нашем примере у первого сотрудника размах вариации зарплаты составляет 20 единиц (710— 690), а у второго - 400 (900—500). На практике размах вариации применяют, в частности, при контроле качества продукции, чтобы, например, размер какого-либо изделия был не меньше и не больше определенных заданных стандартами величин.
Дисперсия - более сложный, но и более точный и часто применяемый показатель. Она представляет собой средний квадрат отклонений вариант от их средней величины, и вычисляется по следующим формулам:
σ2= 
- простая дисперсия для не сгруппированных
данных (когда значения не повторяются)
σ2= 
- взвешенная дисперсия, для
совокупности (ряда) с повторяющимися
значениями.
В данных формулах 
- это средняя (простая или взвешенная), а fi - частоты (веса) соответствующих значений хi.
Иногда вычисляют также среднее квадратическое отклонение (обозначается σ) - это квадратный корень из дисперсии. Оно является обобщающей характеристикой размеров вариации признака в совокупности и показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения. Поскольку среднее квадратическое отклонение выражается в тех же единицах, что и варианты, оно часто используется при характеристике экономических явлений. Чем больше дисперсия или среднее квадратическое отклонение, тем большим разбросом значений признака характеризуется совокупность, следовательно, тем больше ее неоднородность.
В практике очень часто возникают задачи определения однородности какой-либо совокупности, другими словами, выяснения того, насколько похожи друг на друга по определенным характеристикам составляющие совокупность элементы (например, близкие ли суммы тратят на покупки попавшие в выборку посетители магазина, или похожи ли по возрасту покупатели определенного товара). Для решения таких задач используют коэффициент вариации, который представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:
V =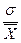 
* 100%
Принято считать, что совокупность количественно однородна, если коэффициент вариации не превышает 33%.
Поскольку коэффициент вариации является относительным показателем и не зависит от конкретных значений, его также можно использовать для решения задач сравнения вариаций различных признаков (например, цены и себестоимости продукции, возраста и дохода покупателей и т.п.).
Анализ и сравнение вариаций может дать много полезной информации для принятия решений. Например, если результаты исследования показывают, что у потребителей некоторого товара весьма небольшой разброс в возрасте, а товар в принципе предназначен для людей практически любого возраста, стоит задуматься над изменением имиджа товара или корректировкой рекламной кампании, чтобы привлечь потенциальных потребителей других возрастных групп.
В заключение остается добавить, что расчет и анализ статистических показателей можно и нужно проводить при помощи компьютера. Во-первых, существуют специальные статистические пакеты программ, а во-вторых, многие статистические показатели и функции реализованы в электронных таблицах Ехсе1.
Подведем итоги
Не нашли, что искали? Воспользуйтесь поиском: