
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Квадратичная функция. Посторенние графика квадратичной функции
Функция, заданная формулой  , где х,у – переменные, а,в,с – заданные числа,
, где х,у – переменные, а,в,с – заданные числа, 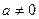 , называется квадратичной.
, называется квадратичной.
Существует несколько способов построения графика квадратичной функции. Опишем два из них.
1 способ. Квадратичную функцию  всегда можно привести к виду
всегда можно привести к виду 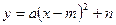 путем выделения полного квадрата.
путем выделения полного квадрата.
Преобразуем квадратный трехчлен  . Имеем:
. Имеем:  Получили формулу
Получили формулу 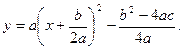
Эта формула имеет вид 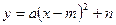 , где
, где  и
и 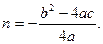
График функции 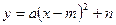 получается из графика функции
получается из графика функции 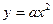 с помощью параллельного переноса, при котором точка
с помощью параллельного переноса, при котором точка  переходит в точку
переходит в точку  . Значит, график любой квадратичной функции
. Значит, график любой квадратичной функции  получается из графика функции
получается из графика функции 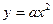 с помощью указанного параллельного переноса.
с помощью указанного параллельного переноса.
2 способ. График функции  есть парабола. Ее вершиной является точка (m; n), где
есть парабола. Ее вершиной является точка (m; n), где  и
и 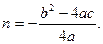 Осью симметрии параболы служит прямая х = т, параллельная оси Оу. При a > 0 ветви параболы направлены вверх, при a < 0 – вниз. Для построения графика квадратичной функции находят координаты нескольких точек соответствующей параболы:
Осью симметрии параболы служит прямая х = т, параллельная оси Оу. При a > 0 ветви параболы направлены вверх, при a < 0 – вниз. Для построения графика квадратичной функции находят координаты нескольких точек соответствующей параболы:
§ абсциссу вершины параболы по формуле 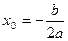 , а ординату –
, а ординату –  ;
;
§ нули функции;
§ точку пересечения параболы с осью Оу – точку (0; с);
§ дополнительные точки, если необходимо.
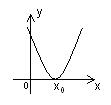
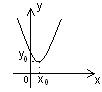
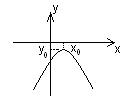
| Д >0 Два корня х1 и х2; график пересекает ось Ох в двух точках. | Д = 0 Один корень х0; график касается оси Ох. | Д < 0 Корней нет; график по одну сторону от оси Ох. | |
| a > 0 | 
|
|
|
| a < 0 | 
| 
|
|
Степенная функция 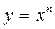
Функция вида 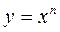 называется степенной функцией с показателем степени n.
называется степенной функцией с показателем степени n.
Если n = 2, то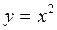 .
1. D(y) = R.
2. E(y) = .
1. D(y) = R.
2. E(y) =  .
3. Функция четная.
4. y=0 при x=0.
5. y > 0 при .
3. Функция четная.
4. y=0 при x=0.
5. y > 0 при 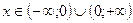 .
6. Функция возрастает на .
6. Функция возрастает на  ;
Функция убывает на ;
Функция убывает на 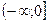 .
7. Функция непрерывна, ограничена снизу нулем. .
7. Функция непрерывна, ограничена снизу нулем.
|
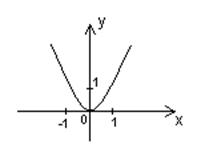
|
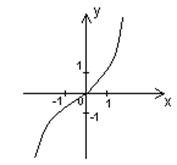
Если n = 3, то 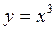 .
1. D(y) = R.
2. E(y) =R.
3. Функция нечетная.
4. y=0 при x=0.
5. y > 0 при .
1. D(y) = R.
2. E(y) =R.
3. Функция нечетная.
4. y=0 при x=0.
5. y > 0 при  ;
y < 0 при ;
y < 0 при 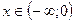 .
6. Функция возрастает на R.
7. Функция непрерывна, неограниченна. .
6. Функция возрастает на R.
7. Функция непрерывна, неограниченна.
|
|
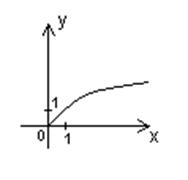
Если 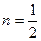 , то , то 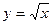 .
1. D (у) = .
1. D (у) =  .
2. Е (у) = .
2. Е (у) =  .
3. Функция ни четная, ни нечетная.
4. y=0 при x=0.
5. y > 0 при x > 0.
6. Функция возрастает на .
3. Функция ни четная, ни нечетная.
4. y=0 при x=0.
5. y > 0 при x > 0.
6. Функция возрастает на  .
7. Функция непрерывна, ограничена снизу нулем. .
7. Функция непрерывна, ограничена снизу нулем.
|
|
Графики степенной функции при различных значениях n представлены в таблице.
n > 0, n  N N
| n < 0, n  Z Z
| ||||
| п - четное | п - нечетное | п - четное | п - нечетное | ||

|

|

|

| ||
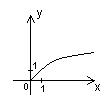
n  R, R, 
| |||||
| п > 1 | 0 < n < 1 | n < 0 | |||

|
|

| |||
Не нашли, что искали? Воспользуйтесь поиском: