Геометрическая прогрессия

Геометрической прогрессией называется числовая последовательность, в которой первый член отличен от нуля, а каждый последующий равен предыдущему, умноженному на некоторое постоянное для данной последовательности число не равное нулю.

Это число называется знаменателем геометрической прогрессии .

Геометрическая прогрессия задается своим первым членом b₁ и знаменателем q.

Любой член геометрической прогрессии можно записать по формуле (формула n-го члена) .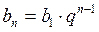

Геометрическая прогрессия возрастает, если или .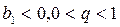

Геометрическая прогрессия убывает, если или .

Если q < 0, то последовательность является ни возрастающей, ни убывающей, т.к. знаки ее членов чередуются.

Характеристическое свойство геометрической прогрессии.

Последовательность чисел является геометрической прогрессией тогда и только тогда, когда каждый ее член, начинается со второго, является средним геометрическим предыдущего и последующего членов или , где n, k N, n 2.

Произведение членов, равноотстоящих от концов прогрессии, есть величина постоянная, т.е. .

Формула суммы n-первых членов геометрической прогрессии

, при q ≠ 1 и при q = 1.

Доказательство:

Сумма n –первых членов геометрической прогрессии равна (1).

Если q = 1, то все члены равны b₁, тогда – что и требовалось доказать.

Если q ≠ 1, то умножим равенство на q, тогда .

По определению геометрической прогрессии

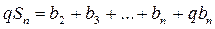(2).

Вычтем равенство (1) из равенства (2), получим ;

;

или , что и требовалось доказать.

Геометрическая прогрессия называется бесконечно убывающей, если |q| < 1.

Суммой бесконечно убывающей геометрической прогрессии называется число, к которому стремится сумма ее n –первых членов при n→∞.

Сумма S бесконечно убывающей геометрической прогрессии равна .

Не нашли, что искали? Воспользуйтесь поиском: