Арифметическая прогрессия

Бесконечной числовой последовательностью называется функция, определенная на множестве натуральных чисел. Ее принято обозначать .

Числовая последовательность, каждый член которой, начиная со второго, равен предшествующему члену, сложенному с одним и тем же числом, называется арифметической прогрессией.

Это число d называется разностью арифметической прогрессии.

d = a₂ – a₁ = a₃ – a₂ = … = a_k – a_k-1 = …

Арифметическая прогрессия задается своим первым членом a₁ и разностью d.

Любой член арифметической прогрессии можно вычислить по формуле (формула n-го члена) .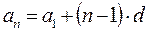

Если d > 0, то арифметическая прогрессия является возрастающей.

Если d < 0, то арифметическая прогрессия является убывающей.

Если d = 0, то все члены арифметической прогрессии равны между собой и она является постоянной последовательностью.

Характеристическое свойство арифметической прогрессии.

Числовая последовательность является арифметической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, является средним арифметическим предшествующего и последующего членов.

или , где n, k N, n 2.

Сумма членов равноудаленных от концов прогрессии есть величина постоянная, т.е. .

Если на плоскости отмечать точки с координатами , то, все эти точки будут лежать на графике функции, задаваемой формулой .

Это означает, что арифметическая прогрессия является линейной функцией, заданной на множестве натуральных чисел N и её можно задать формулой вида 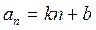, где k, b – числа.

Сумма n – первых членов арифметической прогрессии вычисляется по формуле 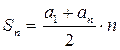или .

Доказательство:

Запишем сумму n –первых членов арифметической прогрессии двумя способами.

Сложим почленно эти равенства.

В каждой скобке стоит сумма вида , где k = 0, 1, …, n-1.

Tаких скобок ровно n, тогда или , что и требовалось доказать.

Не нашли, что искали? Воспользуйтесь поиском: