Оценка погрешности приближенного решения

Для оценки погрешности приближенного вектора 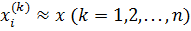, имеют место формулы

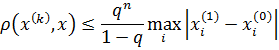
Условие окончания итерационного процесса при нахождении решения с заданной точностью

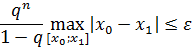
Задание

Дана система уравнений, коэффициенты при неизвестных и сво­бодные члены которой являются точными числами. Найдите ее при­ближенное решение с точностью до ε = 0,5 · 10^-3.

Исходная система:

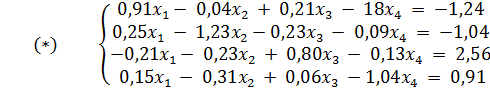
1. Преобразуем систему 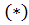к приведенному виду с выполнением условия сходимости итерационной последовательности.

Поменяем в 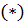местами первую и четвертую строки:

Вычленим единицу из диагонального коэффициента во втором и третьем уравнении, а в четвертом разделим все члены на 18:

(**)

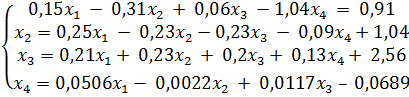
Преобразуем первое уравнение, для чего в системе 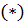умножим четвертую строку на 4 и отнимем от результата вторую:

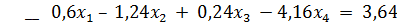
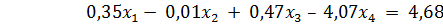
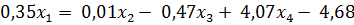= │подставим значения и из (**)│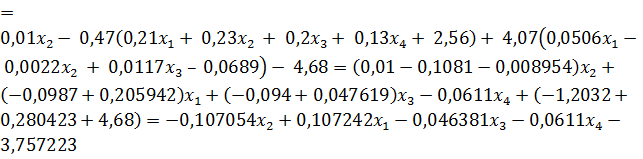

Поделим результат на 0,35 и округлим до четвертого знака после запятой, подставим в (**), после чего получим следующую систему:

Система преобразована к приведенному виду. Теперь наглядно видно, что сумма модулей коэффициентов при 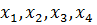меньше единицы:

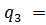0,8; 0,77; 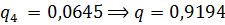, соответственно, итерационный процесс сходится.

2. Взяв в качестве начального приближения вектор свободных членов приведенной системы, найдем вручную первое приближе­ние, затем определим его абсолютную погрешность и проверим ус­ловие окончания итерационного процесса.

Пусть

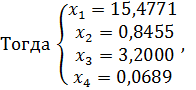
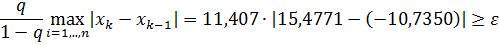
3. Составим программу вычисления приближений до достиже­ния требуемой точности с выводом координаты векторов-приближений и абсолютные погрешности этих векторов в таблицу.

Текст программы:

const

e=0.0005;

n=4;

kolmax=100;

r=11.407;

a:array [1..n,1..n] of real=((0.6936,0.3059,0.1325,0.1746),

(0.25,-1.23,-0.23,-0.09),

(-0.21,-0.23,0.8,-0.13),

(-0.0506,0.0022,-0.0117,1));

b:array [1..n] of real=(10.73492,-1.04,2.56,0.0689);

var

x,xpred: array [1..n] of real;

c:array [1..n,1..n] of real;

d:array [1..n] of real;

eps: real;

key:boolean;

i,kol,j:integer;

begin

repeat

begin

begin

for i:=1 to n do

begin

d[i]:=b[i]/a[i,i];

x[i]:=d[i];

for j:=1 to n do

begin

if i<>j

then

c[i,j]:=-a[i,j]/a[i,i]

else

c[i,j]:=0;

x[i]:=x[i]+c[i,j]*xpred[j];

end;

end;

end;

begin

key:=true;

for i:=1 to n do

begin

if (r*abs(x[i]-xpred[i])) > e

then

key:=false;

end;

end;

eps:=r*abs(x[i]-xpred[i]);

xpred:=x;

kol:=kol+1;

write('vektor x: ');

for i:=1 to n do

write(x[i]:1:4,' ');

writeln (' iteraciya #', kol, ' pogrewnost', eps:1:4);

end;

until (key) or (kol>kolmax);

begin

if kol>kolmax

then

writeln('process rasxoditsya')

else

begin

write('X: ');

for i:=1 to n do

write(x[i]:1:4,' ');

end;

end;

readln;

end.

Результат, выведенный на экран:

vektor x: 15.4771 0.8455 3.2000 0.0689 iteraciya #1 pogrewnost0.7859

vektor x: 14.4756 3.3879 7.5170 0.8876 iteraciya #2 pogrewnost9.3392

vektor x: 12.3235 2.3171 8.1181 0.8819 iteraciya #3 pogrewnost0.0657

vektor x: 12.6824 1.7678 7.2444 0.7824 iteraciya #4 pogrewnost1.1351

vektor x: 13.1166 2.0114 7.1645 0.7915 iteraciya #5 pogrewnost0.1043

vektor x: 13.0221 2.1139 7.3500 0.8120 iteraciya #6 pogrewnost0.2339

vektor x: 12.9363 2.0585 7.3580 0.8092 iteraciya #7 pogrewnost0.0323

vektor x: 12.9599 2.0398 7.3191 0.8050 iteraciya #8 pogrewnost0.0471

vektor x: 12.9767 2.0521 7.3192 0.8058 iteraciya #9 pogrewnost0.0089

vektor x: 12.9710 2.0555 7.3273 0.8066 iteraciya #10 pogrewnost0.0094

vektor x: 12.9678 2.0527 7.3269 0.8064 iteraciya #11 pogrewnost0.0023

vektor x: 12.9691 2.0522 7.3252 0.8063 iteraciya #12 pogrewnost0.0018

vektor x: 12.9697 2.0528 7.3254 0.8063 iteraciya #13 pogrewnost0.0006

vektor x: 12.9694 2.0529 7.3257 0.8064 iteraciya #14 pogrewnost0.0004

vektor x: 12.9693 2.0527 7.3257 0.8063 iteraciya #15 pogrewnost0.0001

vektor x: 12.9694 2.0527 7.3256 0.8063 iteraciya #16 pogrewnost0.0001

vektor x: 12.9694 2.0527 7.3256 0.8063 iteraciya #17 pogrewnost0.0000

X: 12.9694 2.0527 7.3256 0.8063

4. Найдите приближенное решение системы и выпишите его ко­ординаты с верными значащими цифрами.

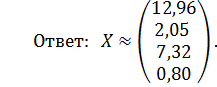
Не нашли, что искали? Воспользуйтесь поиском: