ИНТЕРПОЛИРОВАНИЕ МАТЕМАТИЧЕСКИХ ТАБЛИЦ

Необходимые сведения из теории

Табличная функция

Функция f называется табличной, если на некотором отрезке задана таблица ее значений.

В форме таблиц обычно оформляются результаты эк­спериментальных исследований — эмпирические таблицы. Существу­ют таблицы значений математических функций — математические таблицы. Таблицы используются при приближенном решении мно­гих задач. Например, табличный вид имеет численное решение обык­новенных дифференциальных уравнений.

Для построения таблицы значений функции ) берется от­резок , выбираются точки и каким-либо способом определяются значения ) функ­ции в этих точках. Числа 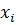называются табличными аргументами, а числа — табличными значениями функции f.

Если табличные аргументы равноотстоящие, т.е. , общее расстояние между ними назы­вают шагом таблицы. В этом случае имеет место формула

Математические таблицы строятся для известных функций и имеют, как правило, постоянный шаг. Среди эмпирических таблиц часто встречаются таблицы с неравноотстоящими аргументами.

Таблич­ные значения находят путем вычислений или измерений и, как пра­вило, являются приближенными числами. Если они все имеют оди­наковую абсолютную погрешность, то она называется погрешнос­тью таблицы. Иногда погрешность на разных участках таблицы различна.

	)
…	…
Табл.1

В зависимости от количества цифр (знаков) в записи значений функции различают табли­цы четырехзначные, пятизначные и т. д. В слу­чае математических таблиц, в которых значе­ния функции записываются только с верпы-ми цифрами, между количеством цифр и точ­ностью таблицы существует неразрывная связь: если на каком-то участке таблицы все значения имеют k цифр после десятичной за­пятой, погрешность этого участка составляет

Необходимо различать табличную функцию и функцию, за­данную таблично (табличным способом). Во втором случае речь идет только о таблице значений, которая является функцией с областью определения, состоящей из конечного множества задан­ных табличных аргументов. Например, областью определения табл.1, понимаемой как «таблично заданная функция», будет множество тогда как включает в себя весь отре­зок . График табл. 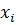1 на плоскости хОу представляет со­бой множество точек {(, ): i = 0, 1, …, n },лежащих на графике функции ).

Интерполирование обычно используется в слу­чае таблиц с небольшим количеством аргументов, поэтому оно боль­ше подходит для локального приближения.

Не нашли, что искали? Воспользуйтесь поиском: