ЗАДАЧІ ДЛЯ САМОСТІЙНОГО РОЗВ’ЯЗУВАННЯ

Задача 1. На певному проміжку часу (зокрема на ранній стадії) розвитку риби її довжина лінійно залежить від віку: , де – довжина, – час, – параметр (коефіцієнт пропорційності), що залежить від виду риби та знаходиться за даними натуральних спостережень. Знайдіть функцію залежності довжини від віку риби, якщо відомо, що довжина виду риби у віці одного року дорівнює 15 см. Дослідіть функцію на парність.

Порада: використайте дану залежність, підставляючи дані в умові задачі; для дослідження на парність використайте умови парності чи непарності функції.

Підказка: 1)виражаємо з даної функції : і знаходимо його значення при заданих умовах; 2) підставляємо замість його значення в дану залежність; 3) у залежність, яку отримали, замість підставляємо і отриману функцію порівнюємо з .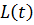

Консультація: 1) виражаємо з даної функції : ;

Знаходимо значення при заданих умовах: (см/рік)

– функція залежності довжини від віку риби

2) , отже 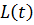– функція непарна.

Відповідь: , функція непарна.

Задача 2. Популяція зайців та вовків виражається формулою , де – кількість популяцій зайців, – кількість популяцій вовків, – параметр, що визначається на підставі даних натуральних спостережень. Знайдіть залежність кількості зайців від кількості вовків, якщо в певний момент часу було зафіксовано та . Що буде графіком даної залежності? Побудуйте графік цієї залежності.

Порада: використайте дану залежність, підставляючи дані в умові задачі; графік будуйте по точкам, беручи додатні значення (тому що кількість зайців або вовків не може бути від’ємною).

Підказка: 1)виражаємо з даної функції : і знаходимо його значення при заданих умовах; 2) підставляємо замість його значення в дану залежність; 3) для побудови графіка візьмемо такі значення і :

Консультація: Із формули виражаємо .

Підставляємо значення і : ;

– функція залежності кількості зайців від кількості вовків при заданих певних умовах.

Графік будуємо по точках. Для побудови графіка функції візьмемо такі значення і :

Графіком даної залежності буде вітка гіперболи, зображена на мал.1:

Мал. 1

Задача 3. Побудуйте графіки функцій на заданих проміжках:

1) +6,

2) ,

3) ,

4) ,

5) ,

6) ,

Відображуватимете отриману фігуру симетрично щодо осі . Малюнок якої комахи ви отримаєте?

Порада: побудуйте першу функцію на заданому проміжку і симетрично відобразіть відносно осі , потім другу функцію будуйте так само і т. д.

Підказка: якщо важко побудувати задану функцію, то починайте з елементарної, наприклад, треба побудувати графік функції +6, то спочатку пунктирною лінією побудуємо графік функції 1) , потім

2) ; 3) ; 4) .

Консультація: графіки функцій зображено на мал. 2

Мал. 2

Відповідь: ми отримали малюнок метелика.

Задача 4. За допомогою графіків функцій в декартовій систем координат створіть власний витвір мистецтва – малюнок павука.

Порада: скористайтеся графіками відомих вам функцій

Підказка: можна використати графіки таких функцій: кола, парабол, прямих тощо.

Консультація: малюнок павука можна створити за допомогою кола і частин парабол. Наприклад мал. 3,

Мал. 3

Задача 5. Реакції організму на два види ліків як функція часу t (час у годинах) складають .Знайти область визначення функцій.

Порада: накладіть обмеження на в і .

Підказка: в і знаменники не дорівнюють нулю.

Консультація: Розглянемо функцію , дана функція еквівалентна . Знаходимо область визначення функції:

ОДЗ: і

,

.

Розглянемо функцію . Знаходимо область визначення функції:

ОДЗ:

Відповідь. для , для .

Задача 6. На мал. 4. зображено демографічні зміни на Мадагаскарі з 2000 по 2014 рік, які аналітично задаються .Користуючись мал. 4, визначте кількість розв’язків рівняння на відрізку .

Мал. 4

Порада: на мал. 4 знайдіть відрізок, заданий в умові; оскільки , то дивимось на точки перетину з віссю .

Підказка: на заданому проміжку дивимось в скількох точках графік функції перетинає вісь .

Консультація: дивимось на проміжок .На цьому проміжку графік функції перетинає вісь 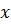у двох точках. Отже, існує 2 розв’язки рівняння на відрізку .

Відповідь: 2 розв’язки.

Задача 7. Відомо, що розчинення мінералів у грунтовій воді протягом року підпорядковується наступного закону в міліграмів на літр. Визначте значення мінералів у квітні та вересні.

Порада: згадайте, яким за рахунком місяцем в році є квітень і вересень; підставте у формулу відповідні дані.

Підказка: замість 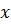у формулу підставте (оскільки квітень є четвертим місяцем в році) і знайдіть відповідне значення мінералів; аналогічно зробіть вересня місяця.

Консультація: Оскільки квітень є четвертим місяцем в році, тому . Значення мінералів у квітні: .

Вересень є дев’ятим місяцем у році, тому . Значення мінералів у вересні: .

Відповідь: значення мінералів у квітні становить , а у вересні – .

Задача 8. Швидкість росту популяції 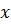задана формулою:

Дослідіть функцію на парність.

Порада: скористайтесь властивістю парності чи непарності функції.

Підказка: у дану формулу замість 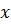підставте і порівняйте отриману функцію з .

Консультація:

.

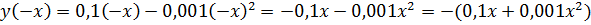Отже, дана функція ні парна, ні непарна.

Відповідь: дана функція ні парна, ні непарна.

Задача 9. Розмір популяції комах у момент часу (в днях) задається формулою . Яка була кількість популяції комах, якщо пройшло годин? Чи правильно, що дана функція спадна?

Порада: у дану формулу підставтедані задачі; для перевірки, чи є дана функція спадною, візьміть ще одне значення .

Підказка: Знайдемо скільки днів у 282 годинах (тому що задано в днях): днів; для перевірки, чи є дана функція спадною, візьміть більше значення , ніж дано в умові, і порівняйте при різних значеннях .

Консультація: Знайдемо скільки днів у 282 годинах:

днів;

Знаходимо кількість популяції комах за днів:

.

Для перевірки, чи є дана функція спадною, візьмемо, наприклад, днів.

.

Дана функція не є спадною. Вона зростаюча, оскільки більшому значенню відповідає більше значення .

Відповідь: кількість популяції комах за 12 днів становить ; дана функція не є спадною.

Задача 10. Кількість хворих під час епідемії грипу змінювалась з часом (вимірюється у днях) від початку вакцинації населення за законом:

. Чи симетричний графік цієї функції відносно осі ?

Порада: використайте властивість парності чи непарності функції.

Підказка: у дану функцію замість підставте і порівняйте отриману функцію з ; якщо парна, то вона симетрична відносно осі , якщо непарна – не симетрична відносно осі .

Консультація: Щоб графік даної функції був симетричний відносно осі , потрібно, щоб функція була парною.

Отже, дана функція є непарною, а значить її графік не симетричний відносно осі .

Відповідь: графік функції не симетричний відносно осі .

РОЗДІЛ 4

НАВЧАННЯ ТЕМИ У КЛАСАХ ЕКОНОМІЧНОГО ПРОФІЛЮ

Не нашли, что искали? Воспользуйтесь поиском: